1、计算题  （09·山东·38）（2）如图所示，光滑水平面轨道上有三个木块，A、B、C，质量分别为mB=mc=2m,mA=m，A、B用细绳连接，中间有一压缩的弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v0运动，C静止。某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同。求B与C碰撞前B的速度。

参考答案：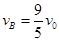

本题解析：：（2）设共同速度为v，球A和B分开后，B的速度为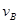,由动量守恒定律有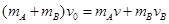,,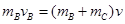联立这两式得B和C碰撞前B的速度为。

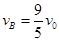本题难度：一般

2、计算题  （10分）如图所示在水平地面上放置质量均为M=400g的木块A和B，一质量为m=50g的子弹以水平速度V0=100m／s射入木块A，当子弹穿出A时，速度V1=80m/s，子弹未穿出木块B，若木块与地面间的动摩擦因数均为μ=0.2。 ( g= 10m/s2)
求:（1）子弹刚射穿木块A时，木块A的速度为多少？
（2）子弹射入B处于相对静止时，木块B的速度为多少？
（3）子弹射入B处于相对静止后，B木块在地面上前进的距离为多大？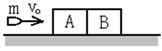

参考答案：（1）1.25m／s
（2）10m／s
（3）25m

本题解析：（1）对整体，根据动量守恒定律：mv0=mv1+2Mv2，?2分?
得：v2=1.25m／s? 1分
（2）对m和B，根据动量守恒定律：mv1+Mv2=(M+m)v，
得：v=10m／s?2分
（3）对m和B，动能定理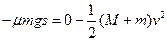，? 3分?
得s=25m?2分

本题难度：简单

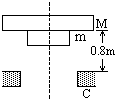
3、简答题  如图所示，两块大小不同、质量分别为M和m的圆形薄板(厚度不计)，半径分别为R和r，M=3m，两板之间用一根长为L=0.4m的轻绳相连结，开始时两板水平放置并叠合在一起处在静止状态，在其正下方0.8m处有一固定支架C，支架上有一半径为R"(r＜R"＜R)的圆孔，圆孔与两薄板中心均在圆孔中心轴线上，今使两板一起无初速自由下落，空气阻力忽略不计．大板与支架C发生没有机械能损失的弹性碰撞，碰撞后，两块板即分离，直到轻绳绷紧，在轻绳绷紧的瞬间，两板便获得共同速度．试求这个共同速度的大小．(g取m/)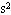

参考答案：
1.5m/s

本题解析：

本题难度：一般

4、其他  

参考答案：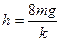

本题解析：开始时A处于平衡状态，有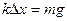　　
　　当C下落ｈ高度时速度为，则有：　　
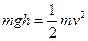
　　C与A碰撞粘在一起时速度为，由动量守恒有：　　
　　当A与C运动到最高时，B对地面无压力，即：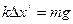　　
　　可得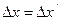：　　所以最高时弹性势能与初始位置弹性势能相等。
　　由机械能守恒有：　　
　　解得：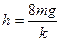

本题难度：困难

5、计算题  （选修3-5选做题）
如图所示，在光滑水平面上有两个并排放置的木块A和B，已知mA=0.5 kg，mB=0.3 kg，有一质量为mC=0.1 kg的小物块C以20 m/s的水平速度滑上A表面，由于C和A、B间有摩擦，C滑到B表面上时最终与B以2.5 m/s的共同速度运动，求：
（1）木块A的最后速度；?
（2）C离开A时C的速度。

参考答案：解：（1）由动量守恒定律得 mCv0=mAvA"+(mC+mB)V?
vA"=2.0m/s
（2）C离开A时，B的速度为2.0m/s
mCv0=(mA+mB)VA+mCvC"?
vC"=4m/s

本题解析：

本题难度：一般