1、简答题  抛出的手雷在最高点时水平速度为10m/s，这时突然炸成两块，其中大块质量300g仍按原方向飞行，其速度测得为50m/s，另一小块质量为200g，求它的速度的大小和方向．

参考答案：设原飞行方向为正方向，则v0=10m/s，v1=50m/s；m1=0.3kg，m2=0.2kg
系统动量守恒：（m1+m2）v0=m1v1+m2v2
整理得：v2=(m1+m2)v0-m1v1m2
代入数据得：v2=-50m/s?
此结果表明，质量为200克的部分以50m/s的速度向反方向运动，其中负号表示与所设正方向相反．
答：它的速度的大小是50m/s和方向和正方向相反．

本题解析：

本题难度：一般

2、计算题  如图所示，一木块位于光滑的水平桌面上，木块上固定一支架，木块与支架的总质量为M．一摆球挂于支架上，摆球的质量为m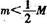，，摆线的质量不计．初始时，整个装置处于静止状态，一质量为m的子弹以大小为v0、方向垂直于纸面向里的速度射人摆球并立即停留在球内．摆球和子弹便一起开始运动．已知摆线最大的偏转角小于90°．在小球往返?运动过程中摆线始终是拉直的，木块未发生转动．
求：（1）摆球上升的最大高度；
（2）摆球在最低处时速度的大小．

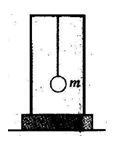
参考答案：
（1）
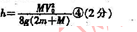
（2）

本题解析：

本题难度：一般

3、选择题  如图所示，在光滑的水平面上，有一质量为M=3kg的薄板和质量 m=1kg的物块，都以v=4m/s的初速度朝相反方向运动，它们之间有摩擦，当薄板的速度为2.4m/s时，物块的运动情况是（?）

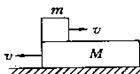
A．做加速运动
B．做减速运动
C．做匀速运动
D．以上运动都有可能

参考答案：A

本题解析：本题考查系统动量守恒的条件和判断应用，因为系统水平方向不受外力，水平方向动量守恒，规定向左为正方向，初动量方向向左，当两个物体共速后动量方向一定向左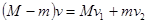，,m速度为0.8m/s为正值，方向向左，两物体速度不同，m受向左的摩擦力，向左加速，A对；

本题难度：简单

4、简答题  质量均为 m 的大小两块薄圆板A和B的中心用长度为L的不可伸长的细线连接．开始时A、B两板中心对齐靠在一起，置于如图所示的水平位置，在A板的下方相距L处，有一固定的水平板C，C板上有一圆孔，其中心与A、B两板的中心在同一竖直线OO"上，圆孔的直径略大小B板的直径，今将A、B两板从图示位置由静止释放，让它们自由下落．当B板通过C板上的圆孔时，A板被C板弹起，假设线的质量、空气阻力、A板与C板的碰撞时间及碰撞时损失的机械能均不计．求：

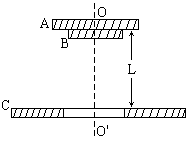
(1)A、C两板相碰后经多少时间细线刚好伸直？
(2)A、B两板间的细线在极短时间内绷紧，求绷紧过程中损失的机械能．

参考答案：
（1）?（2）2mgL

本题解析：


?
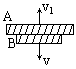
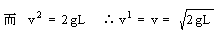之后A向上做竖直上抛运动，B续向下做自由落体运动，设时间t 后细线刚好伸直，则

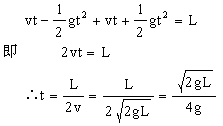
(2)设细线刚好伸直时A的速度为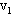，B的速度为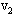．则：

设绷紧后A、B速度为．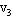

本题难度：一般

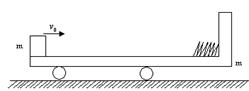
5、计算题  如图所示,在光滑的水平面上有一质量为m,长度为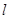的小车，小车左端有一质量也是m可视为质点的物块，车子的右擘固定有一个处于锁定状态的压缩轻弹簧（弹簧长度与车长相比可忽略），物块与小车间动摩擦因数为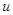，整个系统处于静止。现在给物块一个水平向右的初速度，物块刚好能与小车右壁的弹簧接触，此时弹簧锁定瞬间解除，当物块再回到左端时，与小车相对静止。求：

（1）物块的初速度。
（2）弹簧的弹性势能E。

参考答案：（1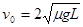）（2）

本题解析：（1）由动量守恒定律得：?（2分）
由能量关系有：?（2分）
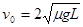解得：?（2分）
（2）物体最终速度为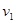，由动量守恒定定律得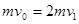：?（2分）
由能量关系有：?（2分）
本题考查动量守恒定律，应用该定律解题时要先选取研究对象，判断动量是否守恒，确定初末状态和动量，列公式求解，本题中系统动量守恒但能量不守恒，系统动能的减小量全部转化为摩擦热

本题难度：简单