1、计算题  (12分)如图12所 示，两平行长直金属导轨置于竖直平面内，间距为L，导轨上端有阻值为R的电阻，质量为m的导体棒垂直跨放在导轨上，并搁在支架上，导轨和导体棒电阻不计，接触良好，且无摩擦．在导轨平面内有一矩形区域的匀强磁场，方向垂直于纸面向里，磁感应强度为B.开始时导体棒静止，当磁场以速度v匀速向上运动时，导体棒也随之开始运动，并很快达到恒定的速度，此时导体棒仍处在磁场区域内，试求：

(1)导体棒的恒定速度；
(2)导体棒以恒定速度运动时，电路中消耗的电功率．

参考答案：(1)v－　向上　(2)

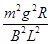
本题解析：(1)设棒速为v′，有
E＝BL(v－v′)? ①
F安＝BIL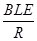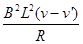＝＝?②
棒受力平衡有：mg＝F安?③
联立得：v′＝v－? ④
方向向上
(2)P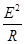＝?⑤
联立①④⑤得：P＝.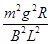

本题难度：简单

2、实验题  如右图所示，A、B两闭合线圈为同样的导线制成，匝数均为10匝，半径RA=2RB，图示区域内有磁感应强度均匀减小的匀强磁场，则A、B线圈中产生的感应电动势之比为EA∶EB=__________，两线圈中感应电流之比为IA∶IB=__________.

参考答案：1∶1?1∶2

本题解析：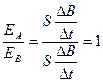
.

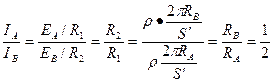本题难度：简单

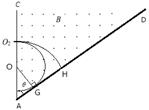
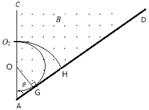
3、计算题  如图所示，匀强磁场B1垂直水平光滑金属导轨平面向下，垂直导轨放置的导体棒ab在平行于导轨的外力作用下从静止开始运动，通过互感，使电压表示数U保持不变。定值电阻的阻值为R，变阻器的最大阻值为。在电场作用下，带正电粒子源从O1由静止开始经O2小孔垂直AC边射入第二个匀强磁场区，该磁场的磁感应强度为B，方向垂直纸面向外，其下边界AD与AC的夹角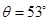。设带电粒子的电荷量为q、质量为m，A端离小孔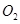的高度为高度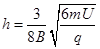，请注意两线圈绕法，不计粒子重力，已知；。

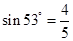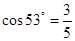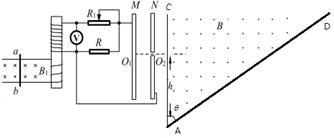
求：（1）为满足要求，试判断金属棒应在外力作用下做何种运动？
（2）调节变阻器的滑动头，使接入电阻为多大时，粒子刚好不会打在AD板上？
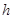（3）调节的滑动头，从题（2）中的位置缓慢移动到接入电阻为处 ，求源源不断的粒子打在AD边界上的落点间的最大距离（用表示）。

参考答案：（1）向左做匀加速直线运动（2）（3）

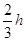
本题解析：（1）要满足要求，金属棒应在外力作用下向左做匀加速直线运动
（2）如图所示，粒子进入B磁场的速度为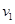，刚好不打在AD板上，圆轨迹半径，

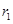则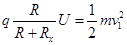①
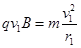②
根据几何关系：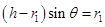
 ④
代入数据，联立①②③④得：
（3）如图，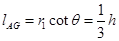
当滑片移到接入电阻为处时，设带电粒子进入磁场时的速度为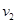，圆轨迹半径为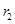则

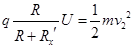       ⑤                   1分
在磁场中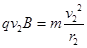：      ⑥           1分
联立④⑤⑥得：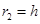 
∴落地点间最大距离：          1分
考点：考查了带电粒子在有界磁场中的运动

本题难度：困难

4、填空题  一个100匝的闭合圆形线圈，总电阻为15.0Ω，面积为50cm2，放在匀强磁场中，线圈平面跟磁感线方向垂直．匀强磁场的磁感应强度B随时间t变化的规律如图（b）所示．设t=0时，B的方向如图（a）所示，垂直于纸面向里．则线圈在0～4×10-3s内的平均感应电动势的大小是______伏；在2s内线圈中产生的热量是______焦．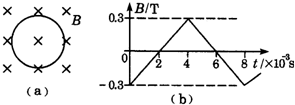

参考答案：根据B-t图中同一条直线磁通量的变化率是相同的，所以电动势为定值，即为E=n△B△tS=100×0.64×103×50×10-4V=75V；
根据在2s内I=ER=△B△tRS，由焦耳定律Q=I2Rt，可知Q=750J．
故答案为：75；750．

本题解析：

本题难度：一般

5、选择题  穿过单匝闭合线圈的磁通量每秒钟均匀连续地增大2Wb,则(　　)。
A．线圈中的感应电动势将均匀增大
B．线圈中的感应电流将均匀增大
C．线圈中的感应电动势将保持2V不变
D．线圈中的感应电流将保持2A不变

参考答案：C

本题解析：穿过单匝闭合线圈的磁通量每秒钟均匀连续地增大2Wb,即，所以根据公式可得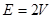：，恒定不变，A错误C正确，电动势不变，则电流恒定，B错误，由于不知道线圈电阻，所以不能确定线圈电流大小，D错误，
故选C
点评：基础题，关键是对公式的正确理解，线圈中磁通量均匀减小，根据法拉第电磁感应定律知，感应电动势为一定值，

本题难度：简单