1、选择题  一个质量为?m?的小球甲以速度?v0?在光滑水平面上运动，与一个等质量的静止小球乙正碰后，甲球的速度变为v，方向不变，那么乙球获得的动能等于（　　）
A．

参考答案：根据动量守恒得，mv0=mv+mv′，解得v′=v0-v．
所以乙球的动能EK=12mv′2=12m(v0-v)2．故B正确，A、C、D错误．
故选B．

本题解析：

本题难度：简单

2、计算题  冰球运动员甲的质量为80.0kg。当他以5.0m/s的速度向前运动时，与另一质量为100kg、速度为3.0m/s的迎面而来的运动员乙相撞。碰后甲恰好静止。假设碰撞时间极短，求：
（1）碰后乙的速度的大小；
（2）碰撞中总机械能的损失。

参考答案：（1）1.0m/s；（2）1400J

本题解析：（1）设运动员甲、乙的质量分别为m、M，碰前速度大小分别为v1、v2，碰后乙的速度大小为v′2，由动量守恒定律有：mv1－Mv2＝Mv′2
解得：v′2＝－v2＝1.0m/s
（2）根据能量守恒定律可知，碰撞中总机械能的损失为：ΔE＝＋－
代入数据解得：ΔE＝1400J

本题难度：一般

3、计算题  （10分)如图所示，在水平光滑直导轨上，静止着三个质量均为m＝1kg的相同小球A、B、C，现让A球以v0＝2m/s的速度向着B球运动，A、B两球碰撞后粘在一起，两球继续向右运动并与C球碰撞，C球的最终速度vC＝1m/s.问：

①A、B两球与C球相碰前的共同速度多大？
②两次碰撞过程中一共损失了多少动能？

参考答案：(1)1m/s　? (2)1.25J

本题解析：(1)A、B相碰，满足动量守恒，则有（2分）
得两球跟C球相碰前的速度v1＝1m/s（1分）
（2）两球与c球碰撞同样满足动量守恒 ?（3分）
两球相碰后的速度 （2分）
两次碰撞损失的动能（2分）

本题难度：一般

4、选择题  不定项选择
如图所示，在水平光滑桌面上有两辆静止的小车A和B，质量之比mA：mB=3∶1。将两车用细线拴在一起，中间有一被压缩的弹簧。烧断细线后至弹簧恢复原长前的某一时刻，两辆小车的（ ? ）

参考答案：B

本题解析：

本题难度：一般

5、计算题   (1)下列说法正确的是?
A．大量氢原子处在n = 3的能级时会辐射出频率连续的三种光，所以氢原子光谱是连续光谱
B．放射性同位素的衰变是指原子核自动转化成新核的过程，有一定的半衰期，遵守质量数和电荷数守恒
C．人类第一次实现的原子核的人工转变核反应方程是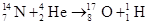
D．卢瑟福通过实验证实了原子核内部存在中子