1、实验题  某同学设计了一个用打点计时器探索碰撞中不变量的实验：在小车A的前端装有橡皮泥，推动小车A使之匀速运动，然后与原来静止在前方的小车B相碰并粘合成一体，继续做匀速运动，他设计的装置如图所示，在小车A的后面连着纸带，电磁打点计时器电源频率为50 Hz，长木板的一端下垫着小木片用以平衡摩擦力。

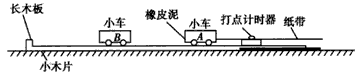
(1)若已得到打点纸带如图所示，并测得各计数点间距标在下图上，A为运动起始的第一个点，则应选________段来计算A碰前速度，应选________段来计算A和B碰后的共同速度。

(2)已测得小车A质量为m1=0.40 kg，小车B的质量为m2=0.20 kg，由以上测量可得：
碰前两车质量与速度乘积之和=________kg·m/s；
碰后两车质量与速度乘积之和=________kg·m/s。
(3)结论____________________________________________。

参考答案：(1)BC，DE
(2)0.420，0.417
(3)在误差允许的范围内，碰前的质量与速度乘积之和等于碰后的质量与速度乘积之和，即碰撞过程中的不变量为质量与速度乘积之和

本题解析：

本题难度：一般

2、简答题  [选修3-5]
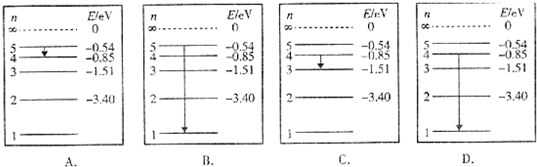
（1）已知处于某一能级n上的一群氢原子向低能级跃迁时，能够发出10种不同频率的光，下列能表示辐射光波长最长的那种跃迁的示意图是

（2）在实验室内较精准地测量到的双β衰变事例是在1987年公布的，在进行了7960小时的实验后，以68%的置信度认出

参考答案：（1）由图示可知，在A所示能级跃迁中释放光子的能量最小，辐射光波的波长越长．
（2）8234Se中有82-34=48个中子，发生双β衰变时有两个中子释放出电子而变为质子，则衰变后中子数为46个；
由质能方程可得，衰变过程中质量亏损△m=Ec2．
（3）以两球组成的系统为研究对象，系统动量守恒，
以A球的初速度方向为正方向，由动量守恒定律得：
mv0=m（-13v0）+2mvB，解得：vB=23v0，
碰后系统的总动能E=12m（-13mv0）2+12×2m（23v0）2=12mv02，
则碰撞前后系统机械能没有损失，则碰撞为弹性碰撞．
故答案为：（1）A；（2）46；Ec2；（3）碰撞为弹性碰撞．

本题解析：

本题难度：简单

3、选择题  如图所示，在光滑水平面上停放着质量为m装有光滑弧形槽的小车，一质量也为m的小球以v0的水平初速度沿槽口向小车滑去，到达某一高度后，小球又返回车右端.则（?）

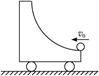
A．小球以后将向右做平抛运动
B．小球将做自由落体运动
C．此过程小球对小车做的功为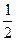mv02
D．小球在弧形槽上升的最大高度为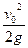

参考答案：BC

本题解析：此过程系统水平方向动量守恒，系统机械能也守恒.小球上升到最高点时，与小车有共同速度v共
则mv0=2mv共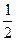，mv02=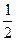2mv共2+mgh得h=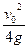
小球回到小车右端有mv0=mv车+mv球
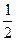mv0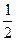2=mv车2+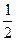mv球2得v车="v0?" v球=0
所以小球做自由落体运动，小球对车做功W=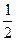mv车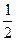2=mv02.

本题难度：简单

4、选择题  在做“验证动量守恒定律”实验时，关于在地面铺纸，下列说法中正确的是（?）
A．铺纸前应查看地面是否平整，无杂物
B．白纸铺在地面上后，在整个实验过程中不能移动
C．复写纸不需要固定在白纸上，测定P点位置时的复写纸，到测定M点位置时，可移到M点使用
D．在地面上铺纸时，复写纸放在下面，白纸放在上面

参考答案：ABC

本题解析：由实验步骤可知A、B正确.只要白纸不移动，移动复写纸不会改变小球落点在白纸上的痕迹.故C也对.

本题难度：简单

5、计算题  如图所示，质量为m的子弹，以速度v水平射入用轻绳悬挂在空中的木块，木块的质量为M，绳长为L，子弹射入木块即停留在木块中，求子弹射入木块的瞬间绳子张力的大小。

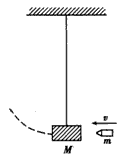
参考答案：解：子弹射入木块，由动量守恒定律，设木块（含子弹）速度为v"，则mv=(M+m)v" ①
木块（含子弹）做圆周运动，由牛顿定律得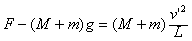 ②
由①②可求得张力大小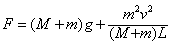

本题解析：

本题难度：一般