1、简答题 如图所示,物体质量为m,由静止开始从A点沿斜面从h1高处下滑到地面,随后又沿另一斜面上滑到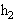 高处的B点停止.若在B点给物体一瞬时冲量,使物体从B点沿着原路返回到A点,需要给物体的最小冲量值是多大?
高处的B点停止.若在B点给物体一瞬时冲量,使物体从B点沿着原路返回到A点,需要给物体的最小冲量值是多大?

参考答案:

本题解析:


本题难度:一般
2、选择题 如图所示,质量为m的物体用细绳车牵引着在水平光滑面上做匀速圆周运动,当拉力为F时,转动半径为R,当外力增大到8F时,物体仍然做匀速圆周运动,其转动半径为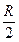 .在此过程中,外力对物体所做的功是(? )
.在此过程中,外力对物体所做的功是(? )

A. FR
FR
B.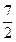 FR
FR
C. FR
FR
D.4FR
参考答案:A
本题解析:由于F= ,8F=
,8F= ,由动能定理
,由动能定理
W= mv22-
mv22- mv12=
mv12= FR,A正确.
FR,A正确.
本题难度:一般
3、计算题 (16 分)某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f. 轻杆向右移动不超过l 时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动l4. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.

(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v’和撞击速度v 的关系.
参考答案:(1) x = f/k?(2)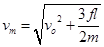 (3)当
(3)当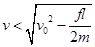 时,
时,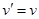 ,当
,当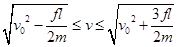 时,
时,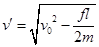
本题解析:(1)轻杆开始移动时,弹簧的弹力 F =kx?①
且 F =f?②
解得 x = f/k?③
设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程
中动能定理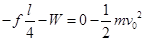 ?④?
?④?
同理,小车以vm 撞击弹簧时?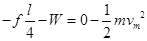 ?⑤?
?⑤?
解得?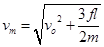 ?⑥?
?⑥?
(3)设轻杆恰好移动时,小车撞击速度为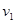 ?
?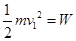 ?⑦
?⑦
由④⑦解得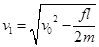
当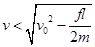 时,
时,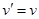 ,
,
当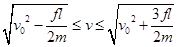 时,
时,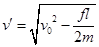
本题难度:简单
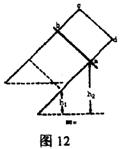
4、选择题 如图12所示,π形光滑金属导轨与水平地面倾斜固定,空间有垂直于导轨平面的磁场,将一根质量为m的金属杆ab垂直于导轨放置。金属杆ab从高度h2处从静止释放后,到达高度为h?1的位置(图中虚线所示)时,其速度为v,在此过程中,设重力G和磁场力F对杆ab做的功分别为WG和WF,那么
A.mv2/2=mgh1-mgh2
B.mv2/2=WG+WF
C.mv2/2>WG+WF
D.mv2/2<WG+WF
参考答案:B
本题解析:分析杆的受力,受重力,弹力,安培力。其中弹力与速度方向时刻垂直,永不做功,根据动能定理,重力和安培力对杆所做的功,等于杆动能的增量,因此选项B正确,其余均错误。
本题难度:简单
5、计算题 如图所示,光滑的水平面上有质量为M的滑块,其中AB部分为光滑的1/4圆周,半径为r,BC水平但不光滑,长为 。一可视为质点的质量为m的物块,从A点由静止释放,最后滑到C点静止,求物块与BC的滑动摩擦系数。
。一可视为质点的质量为m的物块,从A点由静止释放,最后滑到C点静止,求物块与BC的滑动摩擦系数。

参考答案:r /
本题解析:根据能量守恒,可知小球的重力势能全部转化为内能,即 ,所以块与BC的滑动摩擦系数
,所以块与BC的滑动摩擦系数
故答案为
本题难度:一般
Religion is in heart, not in the knees. 信仰在心里,并不在膝下.