1、选择题 地球表面的平均重力加速度为g,地球半径为R,万有引力恒量为G,可以用下式来估计地球的平均密度的大小为( )
A.
B.
C.
D.
参考答案:根据地在地球表面万有引力等于重力,则有:GMmR2=mg
解得地球的质量:M=gR2G
所以地球的平均密度 ρ=MV=3g4πGR.
故选:C.
本题解析:
本题难度:一般
2、选择题 近年来,人类发射的多枚火星探测器已经相继在火星上着陆,正在进行着激动人心的科学探究,为我们将来登上火星、开发和利用火星资源奠定了坚实的基础.如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该运动的周期为T,则火星的平均密度ρ的表达式为(k为某个常量)( )
A.ρ=
B.ρ=kT
C.ρ=kT2
D.ρ=
参考答案:研究火星探测器绕火星做匀速圆周运动,根据万有引力提供向心力,列出等式:
?mr4π2T2=GMmr2? (?r为轨道半径即火星的半径)?
? 得:M=4π2r3GT2-----①
?则火星的密度:ρ=M43πr3-------②
?由①②得火星的平均密度:ρ=3πGT2
?则A B C错误,D正确.
? 故选:D
本题解析:
本题难度:简单
3、简答题 地球绕太阳公转的角速度为ω1,轨道半径为R1,月球绕地球公转的角速度为ω2,轨道半径为R2,那么太阳的质量是地球质量的多少倍.
参考答案:地球与太阳的万有引力提供地球运动的向心力,地球--太阳:GM太M地R21=M地ω21R1… ①
月球与地球的万有引力提供月球运动的向心力,地球--月球:GM地m月R22=m月ω22R2… ②
联立①②得:M太M地=ω21R31ω22R32
答:太阳的质量是地球质量的ω21R31ω22R32倍.
本题解析:
本题难度:一般
4、选择题 宇宙飞船围绕太阳在近似圆周的轨道运动,若其轨道半径是地球轨道半径的4倍,则它们飞船绕太阳运行的周期是( )
A.2年
B.4年
C.8年
D.16年
参考答案:开普勒第三定律中的公式R3T2=k,周期T=
本题解析:
本题难度:一般
5、选择题 假设质量为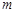 的人造地球卫星在圆轨道上运动,它离地面的高度是地球半径的2倍,地球表面的重力加速度为
的人造地球卫星在圆轨道上运动,它离地面的高度是地球半径的2倍,地球表面的重力加速度为 ,则卫星的(?)
,则卫星的(?)
A.角速度为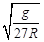
B.线速度为
C.加速度为
D.动能为
参考答案:AC
本题解析:分析:人造地球卫星绕地球做匀速圆周运动,根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式,再结合地球表面重力加速度的公式进行讨论即可.
解答:解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r=3R、地球质量为M,有,F=F向
F=G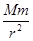 ,F向=m
,F向=m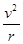 =mω2r=ma
=mω2r=ma
因而,G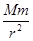 =m
=m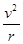 =mω2r=ma
=mω2r=ma
解得v= ?①?ω=
?①?ω=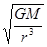 ?②? a=
?②? a=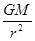 ?③
?③
地球表面重力加速度为g= ?④?根据题意r="R+h=3R" ⑤
?④?根据题意r="R+h=3R" ⑤
由①~⑤式,可以得到,v=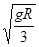 ,
,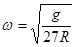 ,a=
,a= ,Ek=
,Ek= mv2=
mv2=
故选AC.
点评:本题关键根据人造卫星的万有引力等于向心力,以及地球表面重力等于万有引力列两个方程求解.
本题难度:一般