1、简答题  如图所示，两只质量均为120kg的小船静止在水面上，相距10m，并用钢绳连接。一个质量为60kg的人在船头以恒力F拉绳，不计水的阻力，求：
（1）当两船相遇时，两船各行进了多少米？
（2）当两船相遇不相碰的瞬间，为了避免碰撞，人从甲船跳向乙船需要对地的最小水平速度为6m/s，计算原来人拉绳的恒力F。

参考答案：（1）s甲=4m，s乙=6m
（2）F=90N

本题解析：（1）由动量守恒定律，得(m甲+m人)v甲=m乙v乙?有(m甲+m人)s甲=m乙s乙
s甲+s乙="10m?" 得，s甲="4m?" s乙=6m
（2）为了避免碰撞，人跳到乙船后系统至少要静止。设人在起跳前瞬间甲船和人的速度为v1，乙船速度为v2，对甲船和人组成的系统由动量守恒得，(m甲+m人)v1=m人×6m/s
得v1="2m/s?" 由动能定理得，Fs甲=(m甲+m人)v12/2?解得F=90N。

本题难度：简单

2、填空题  如图（a）所示，在水平光滑轨道上停着甲、乙两辆实验小车，甲车系一穿过打点计时器的纸带，当甲车受到水平向右的瞬时冲量时，随即启动打点计时器，甲车运动一段距离后，与静止的乙车发生正碰并粘在一起运动，纸带记录下碰撞前甲车和碰撞后两车运动情况如图（b）所示，电源频率为50Hz，则碰撞前甲车运动速度大小为______m/s，甲、乙两车的质量比m甲：m乙=______．

参考答案：碰前甲做匀速运动，由纸带可求得甲车碰前的?速度为v1=s1T=1.2×10-20.02m/s=0.6m/s，
碰后甲、乙一起做运动运动，速度为?v2=s2T=0.8×10-20.02m/s=0.4m/s，
由动量守恒定律得?m甲v1=（m甲+m乙）v2，甲、乙两车质量之比为m甲m乙=v2v1-v2=0.40.6-0.4=21；
故答案为：0.6；2：1．

本题解析：

本题难度：一般

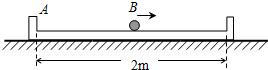
3、填空题  如图，A为内壁长为2m的U型框，框内有一小球B．某时刻开始，小球从框的中点以1m/s的速度向右匀速直线运动，与框右侧挡板碰撞后立刻以相等的速度返回，以后的每次碰撞小球只改变速度方向，且不计碰撞时间．
（1）若框始终静止，则4s内小球与框碰撞的次数为______次．
（2）若框始终以0.5m/s的速度向右匀速直线运动，则3s末小球与框左侧挡板的距离为______m．

参考答案：（1）4s内小球的路程wei：s=v球t=1m/s×4s=4m，
框静止不动，小球从中点开始向右运动，在4s内的路程为4m，小球运动1m与框发生第一次碰撞，在经过2m，共运动1m+2m=3m与框发生第二次碰撞，要发生第三次碰撞需要在运动2m，小球需一共需要运动3m+2m=5m，
在4s内小球运动了4m，因此在4s内小球与框碰撞2次；
（2）小球与框同时向右运动，小球与框的右侧发生第一次碰撞的时间：
t1=s′v小球-v框=11-0.5=2s，
与框碰撞后，小球返回，向左运动，再经过1s小球的路程：
s=v球t=1m/s×s=1m，
框的路程：s′=v框t=0.5m/s×1s=0.5m，
此时小球与框左侧挡板的距离为：
2m-1m-0.5m=0.5m，
即3s末小球与框左侧挡板的距离为0.5m；
故答案为：2；0.5．

本题解析：

本题难度：简单

4、简答题  动量分别为5kg?m/s和6kg?m/s的小球A、B沿光滑平面上的同一条直线同向运动，A追上B并发生碰撞后．若已知碰撞后A的动量减小了2kg?m/s，而方向不变，那么A、B质量之比的可能范围是什么？

参考答案：根据动量守恒定律得
PA+PB=PA′+PB′
又PA′=3kg?m/s，
解得，PB′=8kg?m/s，
碰撞过程系统的总动能不增加，则有P′2A2mA+P′2B2mB≤P2A2mA+P2B2mB
代入得：322mA+822mB≤522mA+622mB①
又由题，碰撞前A的速度大于B的速度，则有
PAmA＞PBmB②
碰撞后A的速度不大于B的速度，则有P′AmA≤P′BmB③
由以上不等式组解得38≤mAmB≤47
答：A、B质量之比的可能范围是38≤mAmB≤47．

本题解析：

本题难度：一般

5、计算题  如图所示，光滑水平地面上停着一辆平板车，其质量为2m，长为L，车右端（A点）有一块静止的质量为m的小金属块．金属块与车间有摩擦，以中点C为界， AC段与CB段动摩擦因数不同。现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，即撤去这个力。已知撤去力的瞬间，金属块的速度为v0，车的速度为2v0，最后金属块恰停在车的左端（B点）。
求:（1）F的大小为多少？?
（2）AC段与CB段动摩擦因数与
的比值。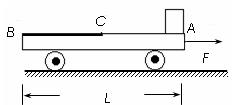

参考答案：(1)设水平恒力F作用时间为t1．
对金属块 a1=μ1g = v0/ t1，得：t1=?……………………………(1分)?
对小车有a2=（F-μ1 mg）/2m="2" v0/t1?得? F=5μ1mg ………… ………… (1分)?
由A→C对金属块?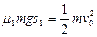?………………………………… (2分)
对小车 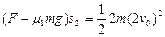?……………………………… (2分)?而 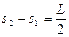?…………………………………………………………(1分)? ∴?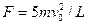………………………………………………… (2分)
(2)从小金属块滑至车中点C开始到小金属块停在车的左端的过程中，系统外力为零，动量守恒，设共同速度为v，由2m×2v0+mv0=（2m+m）v，得v=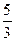v0．……(2分)
由能量守恒有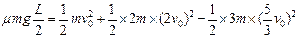?…………(3分)
得?…………………………………………………… (1分)?
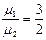∴?…………………………………………………… (1分)

本题解析：略

本题难度：一般