1、计算题 如图所示,光滑水平面左端的固定装置P能根据需要发射和接收质量 、速度为
、速度为 的小球;右边用一长为
的小球;右边用一长为 的不可伸长细线系一质量
的不可伸长细线系一质量 的小球B,绳另一端固定于悬点,起初绳拉直,小球B静止于地面上且对地面的压力恰为零。某时刻让P发射一小球与静止的小球B发生碰撞,假定以后每当小球B经最低点且向右运动时就有一发射小球与小球B碰撞,导致小球B摆动的最大高度逐渐增加,设每次碰撞均没有机械能损失,
的小球B,绳另一端固定于悬点,起初绳拉直,小球B静止于地面上且对地面的压力恰为零。某时刻让P发射一小球与静止的小球B发生碰撞,假定以后每当小球B经最低点且向右运动时就有一发射小球与小球B碰撞,导致小球B摆动的最大高度逐渐增加,设每次碰撞均没有机械能损失, 。求:
。求:
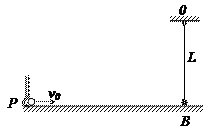
⑴第一次碰撞后,小球B上升的最大高度h;
⑵装置P要发射多少个小球,才能使小球B上升到与悬点等高处。
参考答案:解:(1)当 与静止的B的发生碰撞后,设
与静止的B的发生碰撞后,设 的速度为
的速度为 ,B的速度为
,B的速度为 ,由动量守恒和机械能守恒有
,由动量守恒和机械能守恒有
 ?①?
?①?
 ?②
?②
解得: ?③
?③
B向上摆动过程中,由机械能守恒有,
 ?④
?④
 解得:
解得:  ?⑤
?⑤
(2)当B再摆到最低点向右运动时,P发射的小球第二次与其碰撞,设碰后 的速度为
的速度为 ,B的速度为
,B的速度为 ,由动量守恒和机械能守恒有
,由动量守恒和机械能守恒有
 ?⑥
?⑥
 ?⑦
?⑦
解得: 
当P发射的小球第三次与其碰撞,设碰后B的速度为 ,同理有,
,同理有,
 ?
?
当P发射的小球第n次与其碰撞,设碰后B的速度为 ,同理有,
,同理有,
 ?⑧
?⑧
若让小球B上升到与悬点等高处,则
 ?⑨
?⑨
将 代入,即:?
代入,即:?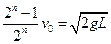
解得: ?
? ?⑩
?⑩
本题解析:略
本题难度:一般
2、选择题 在光滑的水平面上有两个在同一直线上相向运动的小球,其中甲球的质量m1="2" kg,乙球的质量m2="1" kg,规定向右为正方向,碰撞前后甲球的速度随时间变化情况如图所示。已知两球发生正碰后粘在一起,则碰前乙球速度的大小和方向分别为(? )
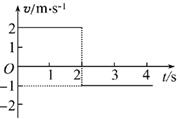
A.7 m/s,向右
B.7 m/s,向左
C.1 m/s,向左
D.1 m/s,向右
参考答案:B
本题解析:根据碰撞过程动量守恒,有 ,其中
,其中 ,
, ,
, ,
, ,带入数据可得
,带入数据可得 ,负号表示速度方向向左,选项B对。
,负号表示速度方向向左,选项B对。
本题难度:简单
3、计算题 如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板.滑板运动到C时被牢固粘连。物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长ι=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度取g.
(1) 求物块滑到B点的速度大小;
(2) 试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功Wf与L的关系,并判断物块能否滑到CD轨道的中点。

参考答案:解:(1)物块从E 点运动到B 点的过程中,只有皮带对物块的摩擦力和重力两个力做功,对该过程应用动能定理得:

(2)物块m和木板M在相互作用的过程中动量守恒,设两者可以达到共同速度,设为V1,该过程中木板运动的位移为X1,两者的相对位移为x。
由动量守恒定律得: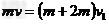
所以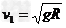
由能量守恒定律得:
对木板应用动能定理得:
当 时,到达C点的整个过程中始终存在滑动摩擦力,所以克服摩擦力做功为:
时,到达C点的整个过程中始终存在滑动摩擦力,所以克服摩擦力做功为:
当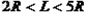 时,物块和木板可以达到相同的速度,此后直到木板碰到C点这一过程中,物块和木板之间是没有摩擦力的,该阶段摩擦力不做功。故这种情况下克服摩擦力做功为:
时,物块和木板可以达到相同的速度,此后直到木板碰到C点这一过程中,物块和木板之间是没有摩擦力的,该阶段摩擦力不做功。故这种情况下克服摩擦力做功为: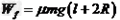 ,与L无关。
,与L无关。
综合两种情况可知,当L=R时,物块克服摩擦力做功最小,这个过程中物块到达C点的速度最大,对这个过程有: 滑上CD轨道后,
滑上CD轨道后,
设上升的最大高度为h,由机械能守恒定律得:
可见物块滑不到CD轨道的中点。
本题解析:
本题难度:困难
4、选择题 斜面体的质量为M,斜面的倾角为α,放在光滑的水平面上处于静止.一个小物块质量为m,以沿斜面方向的速度v冲上斜面体,若斜面足够长,物块与斜面的动摩擦因数为μ,μ>tanα,则小物块冲上斜面的过程中
[? ]
A.斜面体与物块的总动量守恒
B.斜面体与物块的水平方向总动量守恒
C.斜面体与物块的最终速度为
D.斜面体与物块的最终速度为
参考答案:B
本题解析:
本题难度:一般
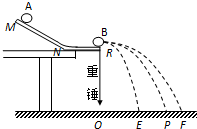
5、简答题 某同学采用如图所示的装置来验证动量守恒定律.图中MN是斜槽,NR为水平槽.实验时先使A球从斜槽上某一固定位置由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹平均位置P;再把B球放在水平槽上靠近槽末端的地方,让A球仍从固定位置由静止开始滚下,与B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹.重复这种操作10次得到10个落点痕迹平均位置E、F.
①若A球质量为m1,半径为r1;B球质量为m2,半径为r2,则______;
A.m1>m2r1>r2 B.m1>m2r1<r2
C.m1>m2r1=r2 D.m1<m2r1=r2
②以下提供的器材中,本实验必需的______.
A.刻度尺B.打点计时器C.天平D.秒表
③A球每次从斜槽上某一固定位置由静止滚下,这是使______.
④设A球的质量为m1,B球的质量为m2,则本实验验证动量守恒定律的表达式为(用装置图中的字母表示)______.
参考答案:①小球在碰撞过程中水平方向动量守恒,由动量守恒定律得:
m1v0=m1v1+m2v2
在碰撞过程中机械能守,由机械能守恒定律得:
12m1v02=12m1v12+12m2v22,
解得:v1=m1-m2m1+m2v0,要碰后入射小球的速度v1>0,即m1-m2>0,
要使两小球发生对心正碰,两球的半径应相等,r1=r2;
②P为碰前入射小球落点的位置,E为碰后入射小球的位置,F为碰后被碰小球的位置,
小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,
碰撞前入射小球的速度v1=OPt,碰撞后入射小球的速度:v2=OEt,碰撞后被碰小球的速度:v3=OFt,
若m1v1=m2v3+m1v2,表明通过该实验验证了两球碰撞过程中动量守恒,
带入数据得:m1?OP=m1?OE+m2?OF,实验需要测量小球的质量,物体的水平位移,因此需要的用天平测小球质量,用刻度尺测小球的水平位移,故选AC;
③小球从斜槽上同一位置由静止滚下,小球到达斜槽末端时的速度相等;
④由②可知,实验需要验证的表达式为:m1?OP=m1?OE+m2?OF.
故答案为:①C;②AC;③A球每次到槽口时有相同的速度;④m1?OP=m1?OE+m2?OF.
本题解析:
本题难度:一般
Dispatch is the soul of business. 迅速是商事之本.