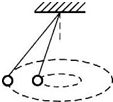
1、简答题  长为L的细线一端系一质量为m的小球，细线的另一端用手拿住，手持线的这端在水平桌面上沿以O点为圆心，R为半径的圆周做匀速圆周运动．达到稳定状态时，细线总是沿圆周的切线方向，如图所示，已知小球与桌面之间的摩擦系数为μ，试求：（1）小球的动能多大？（2）手持线运动中做功的功率多大？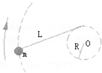

参考答案：

（1）球做匀速圆周运动，动能不变．
小球在水平面上只受拉力T和摩擦力f，由动能定理可知，T和f做功相等：Wf=WT?
f?2πr=T?2πR
根据几何关系，如右图，r=

本题解析：

本题难度：一般

2、选择题  一根长为L的轻杆下端固定一个质量为m的小球，上端连在光滑水平轴上，轻杆可绕水平轴在竖直平面内运动（不计空气阻力）．当小球在最低点时给它一个水平初速度v0，小球刚好能做完整的圆周运动．若小球在最低点的初速度从v0逐渐增大，则下列判断正确的是（　　）
A．小球能做完整的圆周运动，经过最高点的最小速度为

参考答案：A、设轻杆对小球的作用力大小为F，方向向上，小球做完整的圆周运动经过最高点时，对小球，由牛顿第二定律得mg-F=mv2L，当轻杆对小球的作用力大小F=mg时，小球的速度最小，最小值为零，所以A错．
B、由mg-F=mv2L，可得在最高点轻杆对小球的作用力F=mg-mv2L，若小球在最低点的初速度从v0逐渐增大，小球经过最高点时的速度v也逐渐增大，所以轻杆对小球的作用力F先减小后方向增大（先为支持力后为拉力，正负表示力的方向）．由牛顿第三定律可得小球在最高点对轻杆的作用力先减小后增大，因此选项B正确．
C、在最低点，由F-mg=mv2L，可得轻杆对小球的作用力（拉力）F=mg+mv2L，若小球在最低点的初速度从v0逐渐增大，则轻杆对小球的作用力（拉力）一直增大，选项C错．
D、轻杆绕水平轴在竖直平面内运动，小球不是做匀速圆周运动，所以合外力的方向不是始终指向圆心，只有在最低点和最高点合外力的方向才指向圆心，选项D错．
故选B．

本题解析：

本题难度：一般

3、简答题  如图所示，在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场．匀强磁场的磁感应强度为B，方向水平并垂直纸面向外，一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动．（重力加速度为g）
（1）求此区域内电场强度的大小和方向；
（2）若某时刻微粒运动到场中距地面高度为H的P点，速度与水平方向成450，如图所示．则该微粒至少须经多长时间运动到距地面最高点？最高点距地面多高？
（3）在（2）问中微粒运动P点时，突然撤去磁场，同时电场强度大小不变，方向变为水平向右，则该微粒运动中距地面的最大高度是多少？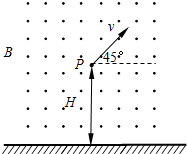

参考答案：

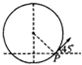
（1）带电微粒在做匀速圆周运动，电场力与重力应平衡，有mg=Eq，即E=mgq，方向竖直向下．
（2）粒子做匀速圆周运动，轨道半径为R，如图所示．qvB=mv2R，
根据几何关系可确定，最高点与地面的距离为Hm=H+R(1+cos450)，
解得Hm=H+mvBq(1+

本题解析：

本题难度：一般

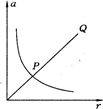
4、选择题  如图所示，P ，Q 是做匀速圆周运动时向心加速度随半径变化的关系图，P 是双曲线，Q 是过原点的直线，则

[? ]
A．质点P的线速度大小不变
B．质点P的角速度大小不变
C．质点Q的角速度随半径变化
D．质点Q的线速度大小不变

参考答案：A

本题解析：

本题难度：简单

5、选择题  如图所示，两个质量不同的小球用长度不等的细线拴在同一点，并在同一水平面内作匀速圆周运动，则它们的（　　）
A．运动线速度一样
B．运动周期相同
C．运动角速度相同
D．向心加速度相同