参考答案:将螺线圈分割为很多小段,每一段近似为一个斜面,由于螺旋线圈等螺距,说明每一小段的斜面倾角相同,设为θ;
根据几何关系,有
sinθ=HL? ①
物体做加速度大小不变的加速运动,根据牛顿第二定律,有
mgsinθ=ma
解得
a=gsinθ? ②
由于物体与初速度和加速度大小相同的匀加速直线运动的运动时间完全相同,故根据位移时间关系公式,有
L=12at2? ③
由①②③解得
t=L
本题解析:
本题难度:一般
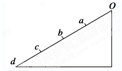
2、选择题 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( ) A.质点由O到达各点的时间之比ta:tb:tc:td=1:2:3:4? ?B.质点通过各点的速率之比va:vb:vc:vd=1: : : :2 :2 C.在斜面上运动的平均速度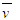 ?=vb ?=vb D.在斜面上运动的平均速度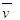 <vb <vb
参考答案:BD
本题解析:
本题难度:简单
3、计算题 做匀加速直线运动的物体,速度从v增加到2v时经过的位移是s,则它的速度从2v增加到4v时所发生的位移是多大?
参考答案:4s
本题解析:
本题难度:一般
4、计算题 (10分)如图所示,长为L=6m、质量M=4kg的长木板放置于光滑的水平面上,其左端有一大小可忽略,质量为m=1kg的物块,物块与木板间的动摩擦因数为0.4,开始时物块与木板都处于静止状态,现对物块施加F=8N,方向水平向右的恒定拉力,设最大静摩擦力等于滑动摩擦力。求:(g取10m/s2)
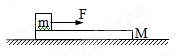
(1)小物块的加速度;
(2)木板的加速度
(3)物块从木板左端运动到右端经历的时间。
参考答案:4m/s2?1m/s2? 2s
本题解析:(1)对小物块进行受力分析有,小物块竖直方向受重力、长木板支持力、水平方向受拉力F和长木板的摩擦力f作用:
在竖直方向有:FN=mg?①
在水平方向有:F f=ma1?②
又因为摩擦力f=μFN?③
由①②③可解得:a1=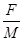 ?μg ?μg
代入数据得:a1=4m/s2
(2)设长木板的加速度为a2,对长木板进行受力分析有
长木板所受合外力F合=μmg=Ma2④
得:a2=1m/s2
⑶令小物块达到长木板右端的时间为t,则根据小物块滑到长木板右端的位移关系有:
L+ a2t2= a2t2= a1t2?代入数据得:t=2s a1t2?代入数据得:t=2s
本题难度:一般
5、简答题 如图所示,两条互相平行的光滑金属导轨位于水平面内,距离为l=0.2米,在导轨的一端接有阻值为R=0.5欧的电阻,在X≥0处有一与水平面垂直的均匀磁场,磁感强度B=0.5特斯拉.一质量为m=o.1千克的金属直杆垂直放置在导轨上,并以v0=2米/秒的初速度进入磁场,在安培力和一垂直于杆的水平外力F的共同作用下作匀变速直线运动,加速度大小为a=2米/秒2、方向与初速度方向相反.设导轨和金属杆的电阻都可以忽略,且接触良好.求:
(1)电流为零时金属杆所处的位置;
(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向;
(3)保持其他条件不变,而初速度v0取不同值,求开始时F的方向与初速度v0取值的关系.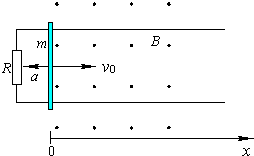
参考答案:(1)感应电动势E=Blv,I=ER∴I=0时?v=0
? 所以x=v022a=1m?
(2)最大电流?Im=BLv0R
I′=Im2=BLv02R
安培力FA=BI′L=B2L2v02R=0.02N?
向右运动时?F+FA=ma
F=ma-FA=0.18N? 方向与x轴相反?
向左运动时F-FA=ma
F=ma+FA=0.22N? 方向与x轴相反?
(3)开始时?v=v0,FA=BImL=B2L2v0R
F+FA=ma,F=ma-FA=ma-B2L2v0R?
∴当v0<maRB2L2=10m/s?时,F>0?方向与x轴相反?
? 当v0>maRB2L2=10m/s?时,F<0?方向与x轴相同.
本题解析:
本题难度:一般
|