1、计算题 (20分)如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连结而成,圆半径必细管内径大得多, 轨道底端与水平地面相切。弹射装置将一个小球(可视为质点)从
轨道底端与水平地面相切。弹射装置将一个小球(可视为质点)从 点水平弹射向?
点水平弹射向? 点并进入轨道,经过轨道后从
点并进入轨道,经过轨道后从 点水平抛出,已知小物体与地面
点水平抛出,已知小物体与地面
 段间的动摩擦因数
段间的动摩擦因数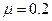 ,不计其它机械能损失,
,不计其它机械能损失,
 段长
段长 ,圆的半径
,圆的半径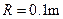 ,小物体质量
,小物体质量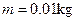 ,轨道质量为
,轨道质量为 ,
,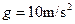 ,求:
,求:
(1)若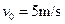 ,小物体从
,小物体从 点抛出后的水平射程;
点抛出后的水平射程;
(2)若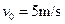 ,小物体经过轨道的最高点时管道对小物体作用力的大小和方向;
,小物体经过轨道的最高点时管道对小物体作用力的大小和方向;
(3)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当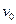 至少为多大时,可出现轨道对地面的瞬时压力为零。
至少为多大时,可出现轨道对地面的瞬时压力为零。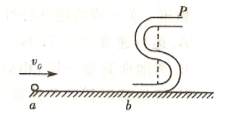
参考答案:(1)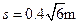
(2)F=11N,方向竖直向下。
(3)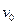 =5m/s
=5m/s
本题解析:(1)小物体运动到p点时的速度大小为,对小物体由 点运动到p点过程应用动能定理得:
点运动到p点过程应用动能定理得:
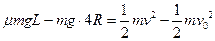 ?(3分)
?(3分)
小物体 自P点做平抛运动,设运动时间为t,水平射程为s,则:
自P点做平抛运动,设运动时间为t,水平射程为s,则:
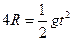 ? (2分)
? (2分)
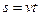 ? (2分)
? (2分)
联立代入数据解得
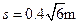 ? (1分)
? (1分)
(2)设在轨道最高点时管道对小物体的作用力大小为F,取竖直向下为正方向
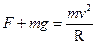 (2分)
(2分)
联立代人数据解得
F="11N?" (1分)
方向竖直向下? (1分)
(3)分析可知,要使小球以最小速度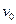 运动,且轨道对地面的压力为零,
运动,且轨道对地面的压力为零,
则小球的位置应该在“S”形轨道的中间位置, (2分)
则有: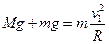 ?(2分)?
?(2分)?
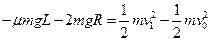 ? (2分)?
? (2分)?
解得: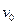 ?=5m/s? (1分)
?=5m/s? (1分)
本题难度:一般
2、选择题 某物体在三个力的作用下动能减少了70J,已知其中一个力做功140J,物体克服另一个力做功60J,则第三个力对物体做的功为: (?)
A. 150J
B.-150J
C.10J
D.-10J
参考答案:B
本题解析:动能减少了70J则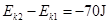 ,一个力做功
,一个力做功 ,物体克服另一个力做功60J,则
,物体克服另一个力做功60J,则 ,根据动能定理
,根据动能定理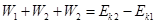 ,所以
,所以 。
。
故选B
点评:物体克服某个力做了功,则这个力就做了负功;动能定理的另一种表述是各个分力做功的代数和等于物体动能的变化量。
本题难度:简单
3、选择题 质量不同而具有相同动能的两个物体,在动摩擦因数相同的水平面上滑行到停止,则( )
A.质量大的滑行的距离大
B.质量大的滑行的时间短
C.质量大的滑行的加速度小
D.它们克服阻力做的功一样多
参考答案:A、根据μmgs=12mv2,解得s=Ekμmg,因为初动能相同,动摩擦因数相同,则质量大的物体滑行的距离小.故A错误.
B、根据牛顿第二定律知,加速度a=μg,知加速度相等,则t=va=
本题解析:
本题难度:简单
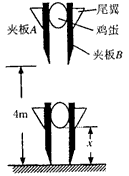
4、计算题 在某中学举办的智力竞赛中,有一个叫做“保护鸡蛋”的竞赛项目。要求制作一个装置,让鸡蛋从两层楼的高度落到地面且不被摔坏。如果没有保护,鸡蛋最多只能从0.1m的高度落到地面而不被摔坏。有一位同学设计了如图所示的一个装置来保护鸡蛋,用A、B两块较粗糙的夹板夹住鸡蛋,A夹板和B夹板与鸡蛋之间的摩擦力都为鸡蛋重力的5倍。现将该装置从距地面4 m的高处落下,装置着地时间短且保持竖直不被弹起。取g=10 m/s2,不考虑空气阻力,求:
(1)若想让鸡蛋直接撞击地面而不被摔坏,其撞地前瞬间的速度最大不能超过多少?
(2)如果使用该装置去保护鸡蛋,鸡蛋夹放的位置离装置下端的距离x至少为多少米?
参考答案:解:(1)如果没有保护,鸡蛋直接撞击地面而不被摔坏,其速度最大为鸡蛋从高度h=0.1m处自由落地时的速度,即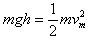 ,
, 
(2)装置从高度H=4 m处落到地面时,鸡蛋的速度为v
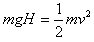 ,
,
装置与地面作用过程中,鸡蛋从离地x处滑到地面时速度只要小于 就不会被摔坏,于是
就不会被摔坏,于是
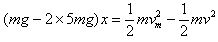
解得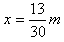
本题解析:
本题难度:困难
5、计算题 如图所示,水平传送带以v=4m/s的速度逆时针转动,两个转轴间的距离L=4m.竖直光滑圆弧轨道CD所对的圆心角θ=370,圆弧半径r=2.75m.轨道末端D点切线水平,且紧贴水平转盘边缘上方.水平转盘半径R=3.6m.沿逆时针方向绕圆心匀速转动.质量m=lkg的小物块.与传送带间的动摩擦因数μ=0.8.将物块轻放到传送带右端,物块从左端水平抛出,恰好沿C点的切线滑入CD轨道,再由D点水平滑落到转盘上.滑块落到转盘上时的速度恰好与落点的线速度相等,滑块立即无相对滑动地随盘转动.取sin37°=0.6,cos37°=0.8。g=10m/s2.求:

(1)物块在传送带上加速运动过程的位移x(相对于地面);
(2)传送带的上表面到水平转盘的竖直高度H;
(3)物块随转盘转动时所爱摩擦力F的大小.
参考答案:(1) x="1m" (2) 1m(3) F=10N
本题解析::
(1)物块在传送带上滑动时,有μmg=ma,
解得a=8m/s2。
由v2=2ax解得加速运动过程相对于地面的位移x=1m。
(2)因x<L,故物块在传送带上将先加速后随传送带一起匀速运动,从左端抛出的速度为v=4m/s。
由题意和几何关系,物块运动到C点的速度v1=v/cosθ=5m/s。
根据机械能守恒定律,mgh1= mv12-
mv12- mv2
mv2
解得h1=0.45m。
由几何关系,h1=ED=r(1-cosθ)=0.55m。
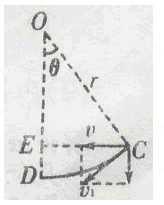
传送带的上表面到水平转盘的竖直高度H= h1+h2=1m。
(3)物块从抛出点到D点过程中,根据机械能守恒定律,mgH= mvD2-
mvD2- mv2
mv2
物块在圆盘上做圆周运动,F=m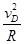 .
.
联立解得物块随转盘转动时所爱摩擦力的大小F=10N.
点评:此题考查牛顿运动定律、速度的分解、机械能守恒定律、圆周运动等知识点。
本题难度:一般