1、计算题  质量m = 20kg的物体以某一初速度滑上倾角θ=370的粗糙斜面，物体能达到斜面上的最大距离L = 20m。已知物体与斜面间的动摩擦因数μ= 0.5。求：（sin370=0.6，cos370=0.8，g = 10m/s2）
（1）物体沿斜面上滑过程中加速度的大小；
（2）物体上滑时初速度的大小；
（3）物体再次回到斜面底端时的动能。

参考答案：（1）10 m/s2（2）20m/s（3）800J

本题解析：（1）由牛顿第二定律可知：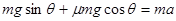
m/s2?（2分）
物体沿斜面上滑过程中加速度的大小为10m/s2
（2）由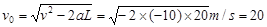，m/s
物体上滑时初速度的大小为20m/s?（3分）
（3）由动能定理得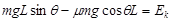

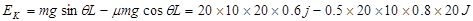
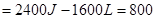J?（3分）
或：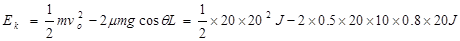
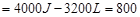J，物体再次回到斜面底端时的动能为800J。

本题难度：简单

2、简答题  如甲图所示，长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处连接，有一质量为2kg的滑块，从A处由静止开始受水平向右的力F作用，F按乙图所示规律变化，滑块与AB和BC间的动摩擦因数均为0.25，重力加速度g取l0m/s2．求：
（1）滑块第一次到达B处时的速度大小；
（2）不计滑块在B处的速率变化，滑块到达B点时撤去力F，滑块冲上斜面，滑块最终静止的位置与B点的距离．（sin37°=0.6）

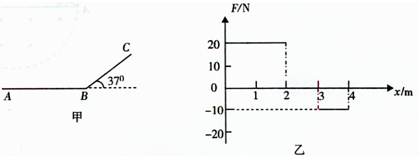
参考答案：（1）由图得：0～2m：F1=20N△X1=2m；?
2～3m：F2=0，△X2=1m；?
3～4m：F3=10N，△X3=1m?
A至B由动能定理：F1?△X1-F3?△X3-μmg（△X1+△X2+△X3）=12mvB2
解得vB=

本题解析：

本题难度：一般

3、简答题  如图所示，质量为m的小球P位于距水平地面高度H处，在水平地面的上方存在一定厚度的“作用力区域”，如图中的虚线部分。当小球进入“作用力区域”后将受到竖直向上的恒定作用力F，F＝5mg，F对小球的作用刚好使从静止释放的小球不与水平地面接触。H＝25 m，g＝10 m / s2。 求：
（1）作用力区域的厚度h＝？
（2）小球从静止释放后的运动是周期性的运动，周期T＝？（即从P点开始运动到又回到P点所用的时间）

参考答案：（1）5m?（2）5s

本题解析：（1）根据动能定理有mgH－Fh＝0·····（2分）
h＝5 m··········（2分）
(2) 设小球在作用力区域上方运动的时间是t1，进入作用力区域的速度是v，在作用力区域内加速度是a，运动的时间是t2，则
t1＝＝2 s···········（2分）
v＝g t1
a＝················（2分）
v＝a t2
g t1＝a t2·······················（2分）
解得t2＝0.5 s····················（2分）
?小球运动的周期T＝2 (t1＋t2)··········（2分）
解得T＝5s···············（2分）

本题难度：一般

4、选择题  如图所示，一个质量为m的圆环套在一根固定的水平长直杆上，环与杆间的动摩擦因数为μ．现给环一个向右的初速度v0，同时对环施加一个竖直向上的作用力F，并使F的大小随v的大小变化，两者关系为F=kv，其中k为常数，则环在运动过程中克服摩擦所做的功大小可能为（　　）
A．

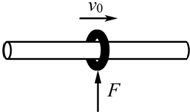
参考答案：根据题意有对于小环的运动，根据环受竖直向上的拉力F与重力mg的大小分以下三种情况讨论：
（1）当mg=kv0时，即v0=mgk时，环做匀速运动，摩擦力为零，Wf=0，环克服摩擦力所做的功为零；
（2）当mg＞kv0时，即v0＜mgk 时，环在运动过程中做减速运动，直至静止．由动能定理得环克服摩擦力所做的功为Wf=12mv20；
（3）当mg＜kv0时，即v0＞mgk 时，环在运动过程中先做减速运动，当速度减小至满足mg=kv时，即v=mgk时环开始做匀速运动．由动能定理得摩擦力做的功
Wf=12mv2-12mv20=m3g22k2-12mv20，
即环克服摩擦力所做的功为12mv20-m3g22k2．
故选ABD

本题解析：

本题难度：简单

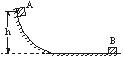
5、选择题  如图所示，一个质量为m的物体从高为h的曲面上一点A处，由静止开始下滑，滑到水平面上B点处停止.若再用平行于接触面的力将该物体从B处拉回到原出发点A处，则需要对物体做功的最小值为（　　）

A．mgh
B．2mgh
C．1.5mgh
D．3mgh

参考答案：B

本题解析：物体由A滑到B时，动能的变化为0，而重力做功为mgh，设摩擦力做的功为Wf，则由动能定理可得，mgh+Wf=0，即Wf=－mgh；如果物体再由B到A，设水平力做的功为W，则W+Wf+(－mgh)=0；故解得W=mgh－Wf=2mgh，B是正确的。

本题难度：一般