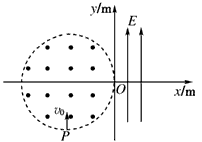
1、计算题  在如图所示的平面直角坐标系中，存在一个半径R＝0.2 m的圆形匀强磁场区域，磁感应强度B＝1.0 T，方向垂直纸面向外，该磁场区域的右边缘与坐标原点O相切。y轴右侧存在电场强度大小为E＝1.0×104 N/C的匀强电场，方向沿y轴正方向，电场区域宽度l＝0.1 m。现从坐标为(－0.2 m，－0.2 m)的P点发射出质量m＝2.0×10－9 kg、带电荷量q＝5.0×10－5 C的带正电粒子，沿y轴正方向射入匀强磁场，速度大小v0＝5.0×103 m/s。重力不计。
(1)求该带电粒子射出电场时的位置坐标；
(2)为了使该带电粒子能从坐标为(0.1 m，－0.05 m)的点回到电场后，可在紧邻电场的右侧一正方形区域内加匀强磁场，试求所加匀强磁场的磁感应强度大小和正方形区域的最小面积。

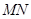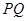2、计算题  （14分）如图甲所示，在水平放置的两平行金属板的右侧存在着有界的匀强磁场，磁场方向垂直于纸面向里，磁场边界和与平行板的中线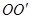垂直。金属板的两极板间的电压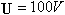，匀强磁场的磁感应强度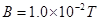。现有带正电的粒子以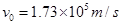的速度沿两板间的中线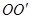连续进入电场，恰能从平行金属板边缘穿越电场射入磁场。已知带电粒子的比荷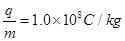，粒子的重力和粒子间相互作用力均可以忽略不计(结果保留两位有效数字)。
(1)求射入电场的带电粒子射出电场时速度的大小和方向。
(2)为使射入电场的带电粒子不会由磁场右边界射出，该匀强磁场区的宽度至少为多大?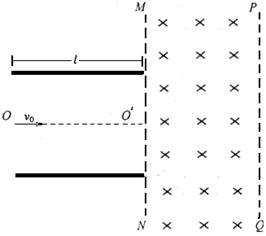

3、计算题  如图所示，一个质量为m=2.0×10-11 kg，电荷量q=+1.0×10-5 C的带电微粒（重力忽略不计），从静止开始经U1=100 V电压加速后，水平进入两平行金属板间的偏转电场中。金属板长L=20 cm，两板间距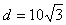cm。求：
(1)微粒进入偏转电场时的速度v0是多大？
(2)若微粒射出偏转电场时的偏转角为θ=30°，并接着进入一个方向垂直于纸面向里的匀强磁场区，则两金属板间的电压U2是多大？
(3)若该匀强磁场的宽度为D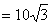cm，为使微粒不会由磁场右边界射出，该匀强磁场的磁感应强度B至少多大？

4、计算题  如图所示,正方形导线框abcd的质量为m、边长为l,导线框的总电阻为R.导线框从垂直纸面向里的水平有界匀强磁场的上方某处由静止自由下落,下落过程中,导线框始终在与磁场垂直的竖直平面内,cd边保持水平.磁场的磁感应强度大小为B,方向垂直纸面向里,磁场上?下两个界面水平距离为l.已知cd边刚进入磁场时线框恰好做匀速运动.重力加速度为g.

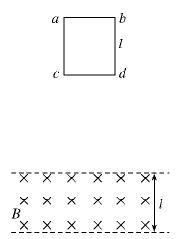
(1)求cd边刚进入磁场时导线框的速度大小;
(2)请证明:导线框的cd边在磁场中运动的任意瞬间,导线框克服安培力做功的功率等于导线框消耗的电功率;
(3)求从导线框cd边刚进入磁场到ab边刚离开磁场的过程中,导线框克服安培力所做的功.

5、计算题  （15分）如图所示，一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后，均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B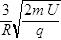＝的匀强磁场中。已知匀强电场的宽度为d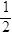＝R，匀强磁场由一个长为2R、宽为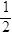R的矩形区域组成，磁场方向垂直纸面向里，粒子间的相互作用和重力均不计。

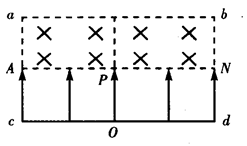
（1）若加速电场加速电压为9U，求粒子在电磁场中运动的总时间；
（2）若加速电场加速电压为U，求粒子在电磁场中运动的总时间。