1、简答题  甲、乙两车做同向直线运动，初始相距S0=10m．已知甲车在前以速度v=4m/s作匀速直线运动，乙车以初速度vo=16m/s开始作匀减速运动，加速度大小为a=4m/s2．试分析：两车相遇几次？何时相遇？

参考答案：设二者经时间t相遇，则V0t-12×at2=Vt+S0
代数字解得：t1=1s；?t2=5s
因为汽车匀减速到零的时间t0=0-v0a=-16-4s=4s．所以t2大于乙车刹车时间，舍去．
1s末乙车的速度为V1=V0-at1=12m/s，它以此速度超过甲车并继续做匀减速直线运动至停止后被甲车追上．乙车在这一阶段发生的位移为：
S1=V212a=18(m)
甲车追上乙车所需要的时间为：t′=S1V=4.5(s)
故第二次相遇的时刻为：
t2=t1+t′=5.5（s）
即二者共相遇两次，相遇时间分别为t1=1s；t2=5.5s．
答：两车相遇两次，相遇的时间分别为1s、5.5s．

本题解析：

本题难度：一般

2、计算题  如图所示，质量为4kg的物体静止于水平面上，物体在大小为20N、方向为与水平方向成37°角斜向上的拉力F作用下，从静止开始沿水平面做匀加速直线运动。物体运动的速度—时间图像如图所示。求：?(取g =" 10" m/s2，sin37° = 0.6,cos37° = 0.8)?


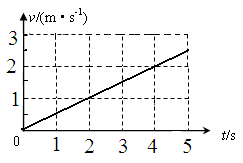
（1）物体的加速度是多大？
（2）物体与水平面间的动摩擦因数为多少？
（3）经过10s时间物体的位移大小为多少？

参考答案：
解：（1）根据物体运动的速度—时间图像可得物体的加速度
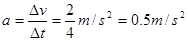?（2分）
（1）物体受力如图所示。根据牛顿第二定律得：
Fcos370―f = ma?（2分）
Fsin370 + N = G?（2分）
又?f =μN?（2分）
由以上三个式子可解得：μ= 0.5?（2分）
(2)根据运动学公式可得：经过10s时间物体的位移大小为
s = at2 = ×0.5×102m =" 25m?" ?（2分）

本题解析：略

本题难度：简单

3、简答题  空间探测器从一星球表面竖直升空，已知探测器质量为2000kg（设为恒量），发动机推力为恒力．探测器升空后发动机因故障而突然关闭，如图所示为探测器从升空到落回星球表面的速度时间变化图象．试求探测器在星球表面达到的最大高度和发动机的推力．现有某同学的解法如下：
由v-t图用计算三角形A0B面积的方法，来计算探测器在星球表面达到的最大高度h，h=

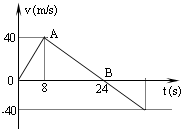
参考答案：计算探测器在星球表面达到的最大高度是正确的，计算发动机的推力有误，应该这样来计算推力：
由v-t图算出探测器在星球上匀减速上升时的加速度g=40-024-8=2.5m/s2、
由牛顿第二定律，得到F-mg=ma，
则F=m（a+g）=2000×（5+2.5）=1.5×104N．
答：发动机的推力为1.5×104N．

本题解析：

本题难度：一般

4、简答题  以18m/s的速度行驶的汽车，紧急刹车后做匀减速直线运动，其加速度大小为2m/s2．
求（1）汽车在刹车后2s末的速度
（2）汽车在刹车后10s内通过的距离
（3）汽车在停止前第2s内的路程．

参考答案：（1）汽车从刹车到停止运动所经历的时间为
t0=0-v0a=0-18-2s=9s＞2s
所以，汽车在刹车后2s末的速度根据速度公式v=v0+at有：
V=18m/s-2m/s2×2s=14m/s?
（2）汽车只能运动9s，汽车在刹车后10s内通过的距离即为前9s内的位移
x=vot+12at2=18×9-12×2×92m=81m?
（3）汽车已运动7s末的速度
v7=v0+at
v7=18m/s-2m/s2×7s
=4m/s?
所以，汽车在停止前第2s内的路程为：
x7=v7t-12at2=4×1-12×2×12m=3m．
答：（1）汽车在刹车后2s末的速度为14m/s．
（2）汽车在刹车后10s内通过的距离81m．
（3）汽车在停止前第2s内的路程为3m．

本题解析：

本题难度：一般

5、选择题  如图所示，在光滑的斜面上放置3个相同的小球（可视为质点），小球1、2、3距斜面底端A点的距离分别为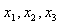，现将它们分别从静止释放，到达A点的时间分别为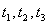，斜面的倾角为θ，则下列说法正确的是

[? ]
A．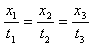
B．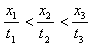
C．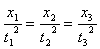
D．若θ增大，则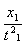的值减小

参考答案：C

本题解析：

本题难度：一般