1、简答题 &n bsp;一传送带装置如图所示，其中AB段是水平的，长度LAB=4m，BC段是倾斜的，长度lBC=5m，倾角为θ=37°，AB和BC在B点通过一段极短的圆弧连接（图中未画出圆弧），传送带以v=4m/s的恒定速率顺时针运转．已知工件与传送带间的动摩擦因数μ=0.5，重力加速度g取10m/s2．现将一个工件（可看做质点）无初速度地放在A点，求：
（1）工件第一次到达B点所用的时间？
（2）工件沿传送带上升的最大高度？
（3）工件运动了23s时所在的位置？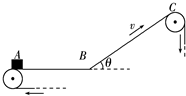

参考答案：（1）工件刚放在水平传送带上的加速度为a1
由牛顿第二定律得μmg=ma1
解得a1=μg=5?m/s2
经t1时间与传送带的速度相同，则t1=va1=0.8?s
前进的位移为x1=12a1t12=1.6?m
此后工件将与传送带一起匀速运动至B点，用时t2=LAB-X1v=0.6?s
所以工件第一次到达B点所用的时间t=t1+t2=1.4?s
（2）设工件上升的最大高度为h，由动能定理得
（μmgcos?θ-mgsin?θ）?hsinθ=0-12mv2
解得h=2.4?m
（3）工件沿传送带向上运动的时间为t3=2hvsinθ=2?s
此后由于工件在传送带的倾斜段运动时的加速度相同，在传送带的水平段运动时的加速度也相同，故工件将在传送带上做往复运动，其周期为T
T=2t1+2t3=5.6?s
工件从开始运动到第一次返回传送带的水平部分，且速度变为零所需时间
t0=2t1+t2+2t3=6.2?s
而23?s=t0+3T
这说明经23?s工件恰好运动到传送带的水平部分，且速度为零．
故工件在A点右侧，到A点的距离x=LAB-x1=2.4?m
答：（1）工件第一次到达B点所用的时间是1.4?s
（2）工件沿传送带上升的最大高度是2.4?m
（3）工件运动了23s时所在的位置是工件在A点右侧，到A点的距离是2.4?m．

本题解析：

本题难度：一般

2、选择题  质点从静止出发做匀加速直线运动，第1秒位移2m，由此可以判断（　　）
A．加速度是4m/s2
B．2秒末瞬时速度4m/s
C．第三秒位移6m
D．4秒内平均速度8m/s

参考答案：A、由x=12at2得，a=2xt2=2×212m/s2=4m/s2．故A正确．
? B、2秒末瞬时速度为v2=at2=4×2m/s=8m/s．故B错误．
? C、第三秒位移x3=v2t+12at2=8×1+12×4×12（m）=10m．故C错误．
? D、根据推论可知，4s内平均速度等于2s末的瞬时速度，为8m/s．故D正确．
故选AD

本题解析：

本题难度：简单

3、计算题  一物体从斜面顶端由静止开始做匀加速运动下滑到斜面底端，在最初3s内位移为s1，最后3s内经过的位移为s2，已知s2+s1＝1.2m，s1∶s2=3∶7，求斜面的长度。

参考答案：1m

本题解析：

本题难度：一般

4、选择题  如图所示，传送带的水平部分长为L，传动速率为v，在其左端无初速释放一小木块，若木块与传送带间的动摩擦因数为μ，则木块从左端运动到右端的时间不可能是（　　）
A．

2L μg D． L 2v 参考答案：①当木块一直做匀加速直线运动． 若木块一直做匀加速直线运动到达右端时的速度还未达到v． 根据牛顿第二定律得，a=μg． 根据L=12at2，解得t= 本题解析： 本题难度：简单 5、简答题  某种类型的飞机起飞滑行时，从静止开始做匀加速运动，加速度大小为4.0m/s2，飞机达到起飞速度80m/s时，突然接到命令停止起飞，飞行员立即使飞机紧急制动，飞机做匀减速运动，加速度的大小为5.0m/s2，请你为该类型的飞机设计一条跑道，使在这种特殊的情况下飞机停止起飞而不滑出跑道，你设计的跑道长度至少要多长？ 参考答案：飞机从静止开始做匀加速运动到离开地面升空过程中滑行的距离为x1，x1=v2-02a1=64002×4m=800m ? 飞机匀减速直线运动的位移x2，x2=0-v22a2=-6400-2×5m=640m 所以跑道的至少长度x=x1+x2=800+640m=1440m． 本题解析： 本题难度：一般