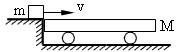
1、计算题  如图所示，质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车，小车的质量为1.6kg，木块与小车之间的摩擦系数为0.2（g取10m/s2）。设小车足够长，求：
（1）木块和小车相对静止时小车的速度。
（2）从木块滑上小车到它们处于相对静止所经历的时间。
（3）从木块滑上小车到它们处于相对静止木块在小车上滑行的距离。

参考答案：解：（1）以木块和小车为研究对象，由动量守恒定律可得：mv0=(M+m)v
所以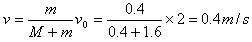
（2）再以木块为研究对象，由动量定理可得-μmgt=mv－mv0

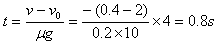
（3）木块做匀减速运动，加速度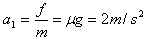
车做匀加速运动，加速度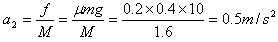
在此过程中木块的位移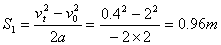
车的位移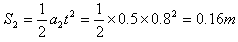
由此可知，木块在小车上滑行的距离为ΔS=S1－S2=0.8m，即为所求

本题解析：

本题难度：困难

2、计算题  如图所示，光滑的水平面上有mA=2kg，mB= mC=1kg的三个物体，用轻弹簧将A与B连接．在A、C两边用力使三个物体靠近，A、B间的弹簧被压缩，此过程外力做功72 J，然后从静止开始释放，求当物体B与C分离时，B对C做的功有多少？

参考答案：18J

本题解析：（1）当弹簧恢复原长时，B与C分离，0=mAvA－（mB+mc）vC?①，
EP=?+?②，?
对C由动能定理得W=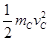－0?③，?
由①②③得W=18J，vA=vC=6m/s．

本题难度：一般

3、计算题  (10分)在光滑水平地面上放有一质量为M带光滑弧形槽的小车，一个质量为m的小铁块以速度V0沿水平槽口滑去，如图所示，求：

(1)铁块能滑至弧形槽内的最大高度：(设m不会从左端滑离M)
(2)小车的最大速度；
(3)若M＝m，则铁块从右端脱离小车后将作什么运动？

参考答案：(1)铁块滑至最高处时，有共同速度V，
由动量守恒定律得：mV0＝(M+m)V?　 ①
由能量守恒定律得：?　　　②
由①②解得：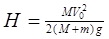
(2)铁块从小车右端滑离小车时，小车的速度最大为V１，此时铁块速度为V２，由动量守恒定律得：　　mv＝MV１　+　mV２?　　?③
由能量守恒定律得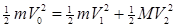：　 　　　　　④
由③④解得：　　
(3)由上面③④解得:　　　?⑤
由已知当M＝m时，由⑤得：V2＝０
又因铁块滑离小车后只受重力，所以做自由落体运动．

本题解析：略

本题难度：一般

4、选择题  在高速公路上发生一起交通事故，一辆质量为1500kg向南行驶的长途客车迎面撞上了一质量为3000kg向北行驶的卡车，碰后两辆车接在一起，并向南滑行了一小段距离后停止，根据测速仪的测定，长途客车碰前以20m/s的速率行驶，由此可判断卡车碰前的行驶速率（?）
A．小于10m/s
B．大于10m/s小于20m/s
C．大于20m/s小于30m/s
D．大于30m/s小于40m/s

参考答案：A．

本题解析：两车碰后连接在一起向南滑行，说明系统的总动量向南，因此碰前客车的动量(方向向南)应大于卡车的动量(方向向北)，即m客v客>m卡v卡，代人数据1500×20>3000×v卡；解得v卡<10m／s，A选项正确．

本题难度：一般

5、简答题  在光滑的高5 m的平台上，有一个质量为1.9 kg的木块，质量为0.1 kg的子弹以20 m/s的水平速度射入木块并留在木块中，求木块落地后的水平位移大小？

参考答案：1 m

本题解析：设子弹初速度方向为正，由动量守恒定律知：
mv0=(M+m)v
v=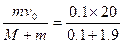m/s="1" m/s
离开平台后木块做平抛运动，下落时间t=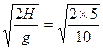s="1" s
故水平位移s="vt=1×1" m="1" m.

本题难度：简单