1、选择题  同步卫星A的运行速率为V1，向心加速度为a1，运转周期为T1；放在地球赤道上的物体B随地球自转的线速度为V2，向心加速度为a2，运转周期为T2；在赤道平面上空做匀速圆周运动的近地卫星C的速率为V3，向心加速度为a3，运转周期为T3．第一宇宙速度为V，则下列说法正确的是（　　）
A．T1=T2＞T3
B．V3＞V2＞V1
C．a3＞a1＞a2
D．V=V2

参考答案：A、同步卫星与地球自转同步，所以T1=T2．
根据开普勒第三定律得卫星轨道半径越大，周期越大，故T1＞T3．故A正确．
B、同步卫星与物体2周期相同，根据圆周运动公式v=2πrT，所以V1＞V2，故B错误．
C、同步卫星与物体2周期相同，根据圆周运动公式a=4π2rT2得a1＞a2，
同步卫星1与人造卫星3，都是万有引力提供向心力，
所以a=GMr2，由于r1＞r3，由牛顿第二定律，可知a3＞a1．故C正确．
D、第一宇宙速度是近地的环绕速度，所以V3=V，而V3＞V1＞V2，故D错误．
故选AC．

本题解析：

本题难度：简单

2、选择题  我国未来将建立月球基地，并在绕月轨道上建造空间站。如图所示，关闭动力的航天飞机在月球引力作用下向月球靠近，并将与空间站在B处对接，已知空间站绕月轨道半径为r，周期为T，万有引力常量为G，下列说法中正确的是

[? ]
A．图中航天飞机正加速飞向B处
B．航天飞机在B处由椭圆轨道进入空间站轨道必须点火减速
C．根据题中条件可以算出月球质量
D．根据题中条件可以算出空间站受到月球引力的大小

参考答案：ABC

本题解析：

本题难度：一般

3、简答题  开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即

参考答案：因行星绕太阳做匀速圆周运动，于是轨道半长轴a即为轨道半径r，根据万有引力定律和牛顿第二定律有
Gm行M太r2=m行(2πT)2r
得：r3T2=K=GM太4π2

本题解析：

本题难度：一般

4、选择题  一艘宇宙飞船在一个星球表面附近，沿着圆形轨道，环绕该星球作近地飞行。若要估测该星球的平均密度，则该宇航员只需要测定的一个参量是：?（?）
A．飞船的环绕半径
B．行星的质量
C．飞船的环绕周期
D．飞船的环绕速度

参考答案：C

本题解析：星球平均密度的估算式为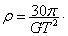所以若要估测该星球的平均密度，则该宇航员只需要测定飞船的环绕周期即可。C正确。故本题选C。

本题难度：一般

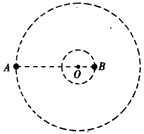
5、计算题  如图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间的距离为L。已知A、B的中心和O三点始终共线，A和B分别在O的两侧。引力常数为G。
（1）求两星球做圆周运动的周期；
（2）在地月系统中，若忽略其它星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T1。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024kg和7. 35×1022kg，求T2与T1两者平方之比。（结果保留3位小数）

参考答案：解：（1）设两个星球A和B做匀速圆周运动的轨道半径分别为r和R，相互作用的引力大小为f，运行周期为T。根据万有引力定律有
? ①
由匀速圆周运动的规律得
? ②
? ③
由题意有? ④
联立①②③④式得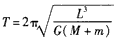? ⑤
（2）在地月系统中，由于地月系统旋转所围绕的中心O不在地心，月球做圆周运动的周期可由⑤式得出
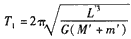? ⑥
式中，M"和m"分别是地球与月球的质量，L"是地心与月心之间的距离。若认为月球在地球的引力作用下绕地心做匀速圆周运动，则
? ⑦
式中，T2为月球绕地心运动的周期。由⑦式得
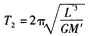? ⑧
由⑥⑧式得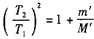
代入数据得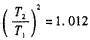

本题解析：

本题难度：困难