1、计算题 AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示。一小球自A点起由静止开始沿轨道下滑。已知圆轨道半径为R,小球的质量为m,不计各处摩擦。求:
(1)小球运动到B点时的动能;
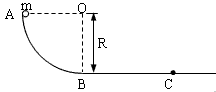
(2)小球下滑到距水平轨道的高度为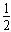 R时的速度大小和方向;
R时的速度大小和方向;
(3)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大?
参考答案:解:(1)根据机械能守恒 Ek=mgR
(2)根据机械能守恒 ΔEk=ΔEp?
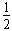 mv2=
mv2=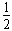 mgR?
mgR?
小球速度大小 v= ,速度方向沿圆弧的切线向下,与竖直方向成30°
,速度方向沿圆弧的切线向下,与竖直方向成30°
(3)根据牛顿运动定律及机械能守恒,在B点?
NB-mg=m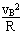 ,mgR=
,mgR=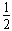 mvB2?
mvB2?
解得 NB=3mg,在C点:NC=mg
本题解析:
本题难度:困难
2、计算题 2010年2月13日在加拿大温哥华冬奥会上,瑞士选手西蒙·阿曼在男子90米跳台滑雪项目上摘取首枚金牌。如图,西蒙·阿曼经过一段加速滑行后从O点水平飞出,落到斜坡上的A点距O点的最远距离为108米。已知O点是斜坡的起点,假设斜坡与水平面的夹角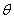 =37°,西蒙·阿曼的质量m=60kg。不计空气阻力。(取sin37°=0.60,cos37°=0.80,g=10 m/s2)求在最远的这一跳中:
=37°,西蒙·阿曼的质量m=60kg。不计空气阻力。(取sin37°=0.60,cos37°=0.80,g=10 m/s2)求在最远的这一跳中:
(1)西蒙·阿曼在空中飞行的时间;
(2)西蒙·阿曼离开O点时的速度大小;
(3)西蒙·阿曼落到A点时的动能。
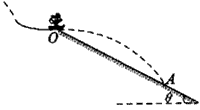
参考答案:解:(1)西蒙·阿曼在竖直方向做自由落体运动,有A点与O点的竖直距离
h=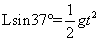
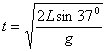 =3.6s
=3.6s
(2)设运动员离开O点的速度为v0,运动员在水平方向做匀速直线运动,即
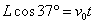
解得
(3)由机械能守恒,取A点为重力势能零点,西蒙·阿曼落到A点的动能为
EKA=mgh+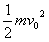
EkA=56160J
本题解析:
本题难度:一般
3、计算题 一轻质细绳一端系一质量为m=0.05kg的小球A,另一端挂在光滑水平轴O上,O到小球的距离为L=0.1m,小球跟水平面接触,但无相互作用,在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,如图所示,水平距离s=2m。现有一滑块B,质量也为m,从斜面上滑下,与小球发生碰撞,每次碰后,滑块与小球速度均交换,已知滑块与挡板碰撞时不损失机械能,水平面与滑块间的动摩擦因数为μ=0.25,若不计空气阻力,并将滑块和小球都视为质点,g取10m/s2,试问:
(1)若滑块B从斜面某一高度h处滑下与小球第一次碰撞后,使小球恰好在竖直平面内做圆周运动,求此高度h;
(2)若滑块B从h'=5m处下滑与小球碰撞后,小球在竖直平面内做圆周运动,求小球做完整圆周运动的次数。
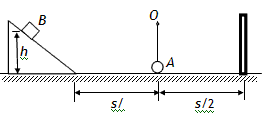
参考答案:
解:(1)小球刚能完成一次完整的圆周运动,它到最高点的速度为v0,
在最高点,仅有重力充当向心力,则有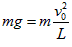 ①
①
在小球从最低点运动到最高点的过程中,机械能守恒,
并设小球在最低点速度为v,则又有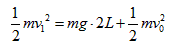 ②
②
解①②有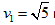 m/s
m/s
滑块从h高处运动到将与小球碰撞时速度为v2,对滑块由能的转化及守恒定律有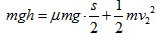 因弹性碰撞后速度交换
因弹性碰撞后速度交换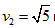 m/s,解上式有h=0.5m
m/s,解上式有h=0.5m
(2)若滑块从h/=5m处下滑到将要与小球碰撞时速度为u,同理有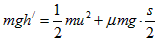 ③
③
解得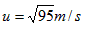
滑块与小球碰后的瞬间,同理滑块静止,小球以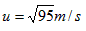 的速度开始作圆周运动,
的速度开始作圆周运动,
滑块和小球最后一次碰撞时速度为至少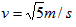
滑块最后停在水平面上,它通过的路程为,同理有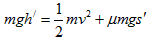 ⑤
⑤
小球做完整圆周运动的次数为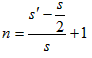 ⑥
⑥
解⑤、⑥得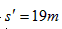 ,n=10次。
,n=10次。
本题解析:
本题难度:困难
4、选择题 在下列过程中机械能守恒的是( )
A.跳伞运动员在空中匀速下落
B.匀速上坡的汽车
C.沿光滑圆弧面下滑的物体
D.沿斜面匀速下滑的物体
参考答案:A、下落过程中,空气阻力做负功,机械能减少,故A错误
B、匀速爬坡的汽车,动能不变,势能增加,故不守恒,故B错误
C、沿光滑圆弧面下滑的物体,只有重力做功,故机械能守恒,故C正确
D、沿斜面匀速下滑的物体,摩擦力做负功,机械能减少,故D错误
故选C
本题解析:
本题难度:一般
5、选择题 一个原长为L的轻质弹簧竖直悬挂着。今将一质量为m的物体挂在弹簧的下端,用手托住物体将它缓慢放下,并使物体最终静止在平衡位置。在此过程中,系统的重力势能减少,而弹性势能增加,以下说法正确的是(?)
A.减少的重力势能大于增加的弹性势能
B.减少的重力势能等于增加的弹性势能
C.减少的重力势能小于增加的弹性势能
D.系统的机械能增加
参考答案:A
本题解析:如果由静止自由释放,则系统机械能守恒,在平衡位置小球速度最大,减小的重力势能等于增加的动能和弹性势能之和,所以A对;手的支持力做负功,机械能减小,D错;
本题难度:简单