1、选择题 假如质量为1 kg的物体置于地心处,物体的重力将是( )
A.9.8 N
B.大于9.8 N
C.无限大
D.零
参考答案:D
本题解析:地球的质量对称地分布于地心的四周,它们对置于地心的物体的引力相互平衡,合力为零,当物体置于地心时,不能直接用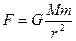 来计算,因公式适用于质点间的相互作用,此时不能用r=0计算而应考虑实际的物理意义和作用效果.
来计算,因公式适用于质点间的相互作用,此时不能用r=0计算而应考虑实际的物理意义和作用效果.
本题难度:简单
2、计算题 已知某行星的质量为M,质量为m的卫星围绕该行星的半径为R,求该卫星的角速度、线速度、周期和向心加速度各是多少?
参考答案: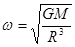 ?
?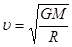 ?
?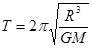 ?
?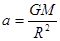
本题解析: 过程中万有引力充当向心力,所以根据万有引力定律和牛顿第二定律可得:
由公式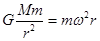 得
得 ,
,
由公式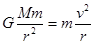 得
得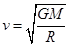 ,
,
由公式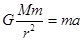 得
得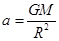 ,
,
根据公式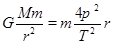 得
得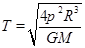 ,
,
点评:天体运动这一模块需要注意公式较多,正确掌握公式是此类题目的关系
本题难度:一般
3、选择题 有一宇宙飞船到了某行星上(该行星没有自转运动),以速度v接近行星赤道表面匀速飞行,测出运动的周期为T,已知引力常量为G,则可得? ( )
A.该行星的半径为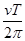
B.该行星的平均密度为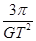
C.无法测出该行星的质量
D.该行星表面的重力加速度为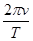
参考答案:ABD
本题解析:由T= 可得:R=
可得:R=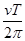 ,A正确;由
,A正确;由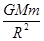 =m
=m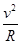 可得:M=
可得:M=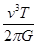 ,C错误;由M=
,C错误;由M=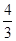 πR3·ρ,得:ρ=
πR3·ρ,得:ρ=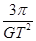 ,B正确;由
,B正确;由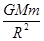 =mg,得:g=
=mg,得:g=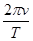 ,D正确.
,D正确.
本题难度:一般
4、计算题 为纪念“光纤之父”、诺贝尔物理学奖获得者高锟的杰出贡献,早在1996年中国科学院紫金山天 文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。已知“高锟星”半径为R,其表面的重力加速度为g,万有引力常量为G,在不考虑自转的情况,求解以下问题:(以下结果均用字母表达即可)
(1)假设“高锟星”为一均匀球体,试求“高锟星”的平均密度;(球体积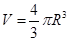 )
)
(2)卫星环绕“高锟星”运行的第一宇宙速度;
(3)假设某卫星绕“高锟星”做匀速圆周运动且运行周期为T,求该卫星距地面的高度。
参考答案:(1)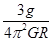 ?(2)
?(2)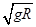 ?(3)
?(3)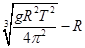
本题解析:(1)由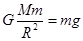 得:
得: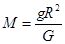
密度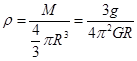
(2)卫星贴近高锟星表面运行时运行速度为第一宇宙速度,
此时卫星的向心加速度a=g,
由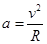 得:第一宇宙速度
得:第一宇宙速度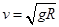 。
。
(3),设高锟星质量为M,卫星质量为m,轨道半径r,
根据题意有: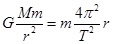 ,又
,又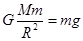 ,联立解得:
,联立解得: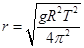 ,
,
所以卫星距地面高度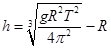
点评:应用万有引力定律解决天体问题时一般要用万有引力等于重力和万有引力等于向心力求解。
本题难度:一般
5、选择题 已知两个质点相距r时,它们之间的万有引力大小为F;若将它们之间的距离变为2r,则它们之间的万有引力大小为( )
A.4F
B.2F
C.
F
D.F
参考答案:根据万有引力定律得:
甲、乙两个质点相距r,它们之间的万有引力为F=GMmr2
若保持它们各自的质量不变,将它们之间的距离增大到2r,
则甲、乙两个质点间的万有引力F′=GMm(2r)2=14F
故选C.
本题解析:
本题难度:一般
He that doth nothing doth ever amiss. 什么都不做,本身就是错.