1、选择题 如图所示,在离地面高为H处以水平速度v0抛出一质量为m的小球,经时间t,小球离水平地面的高度变为h,此时小球的动能为EK,重力势能为EP(选水平地面为零势能参考面)。下列图象中大致能反映小球动能Ek、势能EP变化规律的是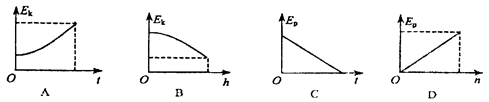
参考答案:AD
本题解析:分析:小球下落过程中只有重力做功,机械能守恒,根据机械能守恒定律列式求解出动能和重力势能的表达式分析讨论.
解答:解:小球下落过程中只有重力做功,机械能守恒,有,mgH+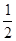 m
m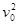 =mgh+EK?①
=mgh+EK?①
平抛运动的竖直分运动为自由落体运动,有,h=H-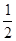 gt2?②
gt2?②
故,Ek=mgH+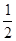 m
m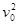 -mgh=mgH+
-mgh=mgH+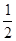 m
m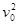 -mg(H-
-mg(H-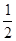 gt2)
gt2)
故A正确,B错误;
Ep=mgh=mg(H-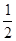 gt2),故C错误,D正确;
gt2),故C错误,D正确;
故选AD.
点评:本题关键是对物体运用机械能守恒定律列方程求解出动能和重力势能的一般表达式进行分析讨论.
本题难度:一般
2、计算题 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为s0,滑块以初速度v0,滑块与斜面间的动摩擦因数为μ, 滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,求滑块经过的总路程.
滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,求滑块经过的总路程.

参考答案:解:滑块最终要停在斜面底部,设滑块经过的总路程为s,对滑块运动的全程应用功能关系,全程所产生的热量为Q=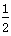 mv02+mgs0sinθ
mv02+mgs0sinθ
又全程产生的热量等于克服摩擦力所做的功,即Q=μmgscosθ
解以上两式可得s=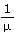 (
( +s0tanθ)
+s0tanθ)
本题解析:
本题难度:一般
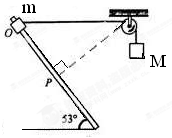
3、选择题 有一个固定的光滑直杆与水平面的夹角为53°,杆上套着一个质量为m=2kg的滑块(可视为质点).用不可伸长的细绳将滑块m与另一个质量为M=2.7kg的物块通过光滑的定滑轮相连接,细绳因悬挂M而绷紧,此时滑轮左侧细绳恰好水平,其长度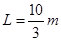 ,p点与滑轮的连线与直杆垂直(如图所示).现将滑块m从图中O点由静止释放,(整个运动过程中M不会触地,g=10m/s2)。则滑块m滑至P点时的速度大小为(?)
,p点与滑轮的连线与直杆垂直(如图所示).现将滑块m从图中O点由静止释放,(整个运动过程中M不会触地,g=10m/s2)。则滑块m滑至P点时的速度大小为(?)
A.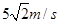
B.5m/s
C.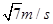
D.2m/s
参考答案:A
本题解析:当滑块滑到P点时,由几何知识可知连接滑块的细线与杆垂直,设滑块此时的速度为u,此时物体M的速度恰好为零,有
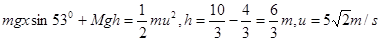
点评:本题难度较大,应以整个系统为研究对象,注意分析两物体发生的位移并不相同
本题难度:一般
4、选择题 一升降机在箱底装有若干个相同弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中,
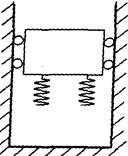
A.升降机的速度不断减小
B.升降机的加速度不断变大
C.先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功
D.到最低点时,升降机加速度的值一定大于重力加速度的值
参考答案:CD
本题解析:略
本题难度:简单
5、简答题 质量为m的物体以100J的初动能从斜面底端A点沿斜面向上匀变速滑行,到斜面上B点时,物体动能减少了80J,机械能减少了32J,则当物体回到A点时物体的动能是多少?
参考答案:设斜面倾角为θ,由A到B,物体动能减少80J,机械能减少32J,由动能定理和能量转化与守恒定律,(机械能减少等于克服摩擦力做功),则有:
-(mgsinθ+f)sAB=0-80
fsAB=32
则重力势能增加了:mgsinθsAB=48J
得:mgsinθf=32,
设物体由B再向上滑行s到达最高点,
由动能定理:-(mgsinθ+f)s=0-20,
得:mgssinθ=12,
fs=8
物体到达最高点,重势能为(48+12)J=60J向上滑行到达最高点的过程中,克服摩擦力做功:(32+8)J=40J,物体从最高点(下滑)回到A点,重力做功60J,克服摩擦力做功40J,则当物体回到A点时物体的动能是20J.
答:当物体回到A点时物体的动能是20J.
本题解析:
本题难度:一般