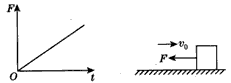
1、选择题  如图所示，放在光滑水平面上的木块以速度v0向右做匀速直线运动，现有一向左的水平力F作用在木块上，且力F与时间t成正比变化，在这个过程中，能正确描述木块运动情况的图象是下图中的（向右为正方向）

[? ]
A.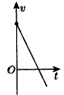
B.
C.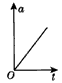
D.

参考答案：BC

本题解析：

本题难度：一般

2、计算题  （14分）如图所示，质量mA=1kg的小物块以向右VA=4.0m/s的初速度滑上质量mB=1.0kg以向左初速度VB=5.0m/s的长木板，已知A、B之间的动摩擦因数μ1="0.20" ，B与地面之间的动摩擦因数μ2=0.40，整个过程中小物块并未从长木板上滑下，g取10 m/s2。则：
（1）求小物块A刚滑上长木板B时，小物块与长木板的加速度。
（2）求从小物块A刚滑上长木板B到二者刚好相对静止时小物块的位移的大小。

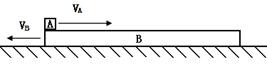
参考答案：（1）小木块加速度为2.0m/s2，方向向左；
长木板加速度为10m/s2，方向向右
（2）4m

本题解析：
（1）以A作为研究对象，由牛顿第二定律得：
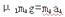?（2分）得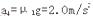?（1分）方向向左（1分）
以B作为研究对象，由牛顿第二定律得：
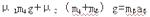?（2分）?得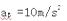（1分）方向向右（1分）
（2）由题意可知A、B都做减速运动，设B的速度先变为0时且所用时间为t1，
则对B：?得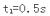：?此时A的速度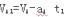?得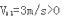所以假设成立。
此后A对B的摩擦力小于地面对B的摩擦力，所以B停止运动，A以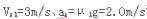继续做减速运动，直至停止运动，所以整个过程中，A做匀减速运动，（2分）
由运动学公式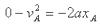：（3分）?代入数据解得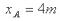：（1分）

本题难度：一般

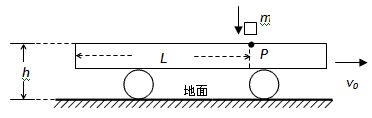
3、计算题  如图所示，水平地面上的平板车在外力控制下始终做匀速直线运动，速度大小v0=4m/s，方向水平向右。某时刻将一质量为m=1kg的小滑块（可视为质点）轻放到车面上的P点，P点与平板车左端相距L=3m，车面距地面的高度h=0.8m，滑块与车面间的动摩擦因数μ=0.2，取g=10 m/s2，求：
（1）小滑块轻放到P点时的加速度a1；
（2）滑块运动至车的最左端时的速度多大？
（3）滑块刚落至地面时滑块与车左端的水平距离多大？

参考答案：解：（1）m/s2
? 方向水平向右。
（2）假设滑块一直匀加速至车的左端，运动时间为t1，
则：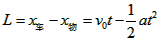
所以，解得：（舍去）
当t1=1s时，滑块的速度为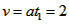：m/s＜v0
所以，滑块运动到车的最左端的速度为2m/s。
（3）滑块离开车后做平抛运动，下落时间为t，则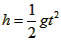，t=0.4s
滑块落地时与车的左端的水平距离为：。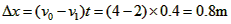

本题解析：

本题难度：一般

4、计算题  如图所示，竖直放置的光滑半圆形轨道与动摩擦因数为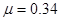的水平面AB相切于B点，A、B两点相距L=2.5m，半圆形轨道的最高点为C，现将一质量为m=0.1kg的小球（可视为质点）以初速度v0=9m/s沿AB轨道弹出，g=10m/s2。求

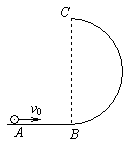
（1）小球到达B点时的速度大小及小球在A、B之间的运动时间；
（2）欲使小球能从最高点C水平抛出，则半圆形轨道的半径应满足怎样的设计要求？
（3）在满足上面（2）设计要求的前提下，半圆形轨道的半径为多大时可以让小球落到水平轨道上时离B点最远？最远距离是多少？

参考答案：（1）8 m/s ?s ?（2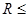）1.28m（3）R=0.8m，最远距离3.2m

本题解析：（原创，考查平抛运动、牛顿第二定律、匀变速直线运动公式、动能定理，参考分值15分）
（1）小球从A到B，加速度大小为m/s2?（1分）
由运动学公式得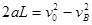（1分）
解得8 m/s（1分）
在 A、B之间的运动时间?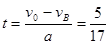s（1分）
（2）若小球恰能到达C点，由牛顿第二定律得mg 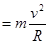（1分）
小球从B到C，由动能定理得?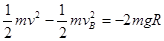（2分）
解得=1.28m（1分）
所以，欲使小球能从C点水平抛出，则半圆形轨道的半径应 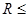1.28m（1分）
（3）小球从C点做平抛运动，由平抛运动的规律得2R =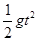，x=vt（2分）
由（2）的求解知
解得x=（1分）
当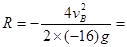0.8m（<1.28m，能够到达C点）时水平射程最远（2分）
最远距离为xm=3.2m（1分）

本题难度：一般

5、选择题  小球以6m/s的速度水平抛出，落到水平地面时的速度为10m/s，取g=10m/s2，小球从抛出到落地的时间及水平位移分别是
A.0.8s；4.8m
B.1s；4.8m
C.0.8s；3.2m
D.1s；3.2m

参考答案：A

本题解析：根据运动的合成与分解，平抛运动分解为水平匀速直线运动和竖直自由落体运动；
落地速度为10m/s，根据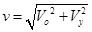，解得，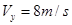
又因为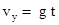：，所以t=0.8s，故BD错误；
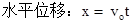=4.8m。故A对，C错；所以答案选A。
此题考查平抛运动的解决方法，利用运动的合成与分解。

本题难度：一般