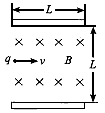
1、选择题 长为L、间距也为L的两平行金属板间有垂直纸面向里的匀强磁场,如图所示,磁感应强度为B。今有质量为m、电荷量为q的正离子从平行板左端中点以平行于金属板的方向射入磁场。欲使离子不打在极板上,入射离子的速度大小应满足的条件是?
[? ]
A.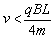
B.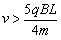
C.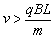
D.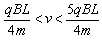
参考答案:AB
本题解析:
本题难度:一般
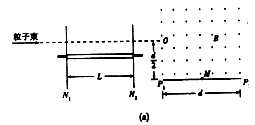
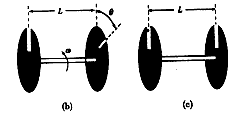
2、计算题 如图(a)所示,为某同学设想的粒子速度选择装置,由水平转轴及两个薄盘N1、N2构成,两盘面平行且与转轴垂直,相距为L,盘上各开一狭缝,两狭缝夹角θ可调(如图(b));右为水平放置的长为d的感光板,板的正上方有一匀强磁场,方向垂直纸面向外,磁感应强度为B一小束速度不同、带正电的粒子沿水平方向射人N1,能通过N2的粒子经O点垂直进入磁场O到感光板的距离为d/2,粒子电荷量为q,质量为m,不计重力
(1)若两狭缝平行且盘静止(如图(c)),某一粒子进入磁场后,竖直向下打在感光板中心点M上,求该粒子在磁场中运动的时间t;
(2)若两狭缝夹角为θ0,盘匀速转动,转动方向如图(b)要使穿过N1、N2的粒子均打到感光板P1P2连线上,试分析盘转动角速度ω的取值范围(设通过N1的所有粒子在盘旋转一圈的时间内都能到达N2)。
参考答案:解:(1)粒子运动半径为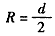 ①
①
由牛顿第二定律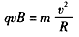 ②
②
匀速圆周运动周期 ③
③
粒子在磁场中运动时间 ④
④
(2)如图所示,设粒子运动临界半径分别为R1和R2
设粒子临界速度分别为v1和v2,
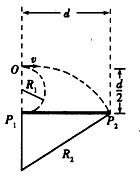
 ⑤
⑤
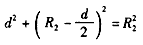
 ⑥
⑥
由②⑤⑥式,得
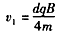 ⑦
⑦
 ⑧
⑧
若粒子通过两转盘,由题设可知
 ⑨
⑨
联立⑦⑧⑨,得
对应转盘的转速分别为
 ?⑩
?⑩
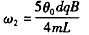

粒子要打在感光板上,需满足条件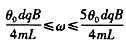

本题解析:
本题难度:困难
3、简答题 图中MN表示真空室中垂直于纸面的平板,它的一侧有匀强磁场,磁场方向垂直纸面向里,磁感应强度大小为B.一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁场区域,最后到达平板上的P?点.已知B、v以及P?到O的距离l.不计重力,求此粒子的电荷q与质量m?之比.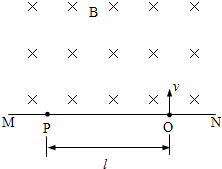
参考答案:粒子初速v垂直于磁场,粒子在磁场中受洛伦兹力而做匀速圆周运动,
设其半径为R,由洛伦兹力公式和牛顿第二定律,有qvB=mv2R
因粒子经O点时的速度垂直于OP.故OP?是直径,l=2R
由此得?qm=2vBl
本题解析:
本题难度:一般
4、选择题 若质子和α粒子以相同的速度垂直射入某一匀强磁场,则质子和α粒子在匀强磁场中运动的?(?)
A.轨道半径之比为1∶1
B.轨道半径之比为1∶2
C.周期之比为1∶1
D.周期之比为2∶1
参考答案:B
本题解析:答案应该为:B
带电粒子以一定速度垂直进入磁场中,受到洛伦兹力作用下做匀速圆周运动.运动轨迹的半径由磁感应强度、电量、质量及速度决定.而运动轨迹的周期与磁感应强度、电量、质量有关,却与速度无关.
解:质子(11P)和α粒子(42He)以相同的速度垂直进入同一匀强磁场中,均做匀速圆周运动.则由轨迹的半径为:R= 得:
得:
半径与这两粒子的质量与电量的比值成正比.即RP:Rα=1:2
而周期公式:T=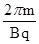 ?得:
?得:
同期也与这两粒子的质量与电量的比值成正比.即TP:Tα=1:2
故选:B
本题难度:简单
5、选择题 三个速度大小不同的同种带电粒子,沿同一方向从图中长方形区域的匀强磁场左上角射入,当它们从下边缘飞出磁场时与入射方向的偏角分别为90°、60°、30°,则它们在磁场中运动的时间之比为
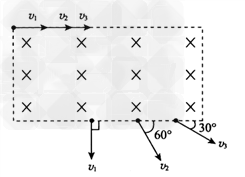
[? ]
A.1:1:1
B.1:2:3
C.3:2:1?
D.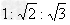
参考答案:C
本题解析:
本题难度:一般