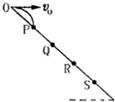
1、计算题  如图所示，一个半径为R的光滑圆弧轨道APB竖直固定放置，PQ为其竖直对称轴，∠AOQ与∠BOQ都等于θ。现让一可看做质点的小球在轨道内侧运动，当其冲出A点后恰好可以从B点再进入轨道，所以此运动可以周而复始进行。已知小球质量为m，重力加速度为g，试求：

(1)小球离开轨道后的最高点距直线AB的距离；
(2)若要小球在最低点时对轨道的压力最小，θ应为多少？对应的最小压力为多少？

参考答案：(1)h=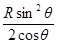?(2)Nm=

本题解析：(1)物体刚刚冲出A点时，将物体速度分解有

v1=vcosθ? (1)
v2=vsinθ? (2)
在抛出到最高点过程中，水平方向为匀速直线运动，有
Rsinθ=v1t? (3)
竖直方向为匀变速直线运动，末速度为零，时间逆向来看是初速度为0的自由落体运动，有
v2=gt? (4)
h=? (5)
由以上(1)(2)(3)(4)可解得
v=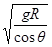? (6)
t=? (7)
由(5)得
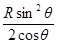h=?(8)
(2)设物体在最低点的速度为v"，则物体在从A到最低点过程中，根据动能定理
mgR(1+cosθ)=? (9)
在最低点，由向心力公式，有
N-mg=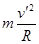? (10)
由(6)(9)(10)得
N=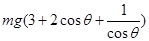? (11)
分析知当θ=45?时，N最大为
Nm=? (12)
评分标准：
(1)问6分，(3)(4)各2分，(5)(8)各1分。
(2)问6分，(9)(10)各2分，结果2分。
本题考查斜上抛运动规律，水平方向不受外力做匀速直线运动，竖直方向只受重力作用做竖直上抛运动，到达最高点时竖直分速度减小到零，先把初速度分解，由水平方向匀速运动求得运动时间，再由竖直方向的运动求得竖直分速度，由竖直上抛运动求得竖直高度，从抛出到最低点，由动能定理列出公式，在最低点，由支持力和重力的合力提供向心力，写出支持力的表达式，再由数学方法求得最大值

本题难度：一般

2、选择题  如图所示，具有圆锥形状的回转器（陀螺），半径为R，绕它的轴在光滑的桌面上以角速度ω快速旋转，同时以速度v向左运动，若回转器的轴一直保持竖直，为使回转器从左侧桌子边缘滑出时不会与桌子边缘发生碰撞，v至少应等于

[? ]
A．?
B．
C．?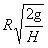
D．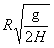

参考答案：D

本题解析：

本题难度：一般

3、简答题  如图所示，ABDO是处于竖直平面内的固定光滑轨道，AB是半径为R=15m的

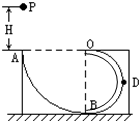
参考答案：（1）设小球能到达O点，由P到O，机械能守恒，设到O点的速度为 vO，则
?mgH=12mV02?
所以V0=

本题解析：

本题难度：一般

4、选择题  在高度为h的同一位置向水平方向同时抛出两个小球A和B，若A球的初速度vA大于B球的初速度vB，则下列说法中正确的是(　　)
A．A球比B球先落地
B．在飞行过程中的任一段时间内，A球的水平位移总是大于B球的水平位移
C．若两球在飞行中遇到一堵墙，A球击中墙的高度大于B球击中墙的高度
D．若两球在飞行中遇到一堵墙，A球击中墙的高度小于B球击中墙的高度

参考答案：BC

本题解析：研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，两个方向上运动的时间相同．
A、平抛运动的运动时间是由竖直高度决定的，AB两个球的高度是相同的，所以它们的运动的时间也是相同的，所以A错误．
B、由于A球的初速度vA大于B球的初速度vB，所以在飞行过程中的任一段时间内，A球的水平位移总是大于B球的水平位移，所以B正确．
C、遇到墙时，AB两球的水平位移是相同的，由于A球的初速度vA大于B球的初速度vB，所以A的运动时间要比B的运动时间短，再根据竖直方向的自由落体规律可知，A下落的距离小，所以A球击中墙的高度大于B球击中墙的高度，所以C正确．
D、AB两个球在竖直方向上的运动的情况是一样的，竖直方向的速度的大小始终相同，但是A球的初速度vA大于B球的初速度vB，所以A球的速率总是大于B球的速率，所以D错误．
故选BC．
点评：本题就是对平抛运动规律的考查，平抛运动可以分解为在水平方向上的匀速直线运动，和竖直方向上的自由落体运动来求解．

本题难度：一般

5、选择题  如图所示，斜面上O、P、Q、R、S五个点，距离