1、计算题 如图,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10米,BC长1米,AB和CD轨道光滑。一质量为1千克的物体,从A点以4米/秒的速度开始运动,经过BC后滑到高出C点10.3m的D点速度为零。求:(g=10m/s2)
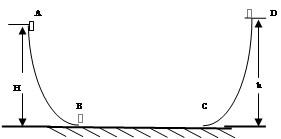
(1)物体与BC轨道的滑动摩擦系数;
(2)物体第5次经过B点时的速度;
(3)物体最后停止的位置(距B点)。
参考答案:(1)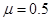 ?(2)13.3(3)0.4m
?(2)13.3(3)0.4m
本题解析:(1)分析从A到D过程,由动能定理得
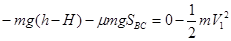 ?解得
?解得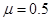
物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
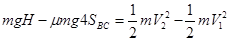 ?解得
?解得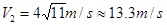
分析整个过程,由动能定理得 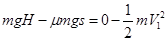 (2分) 解得s=21.6m
(2分) 解得s=21.6m
所以物体在轨道上来回了20次后,还有1.6m,故离B的距离为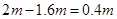
点评:运用动能定理解题,关键是选择好研究的过程,研究的过程选取得好,会对解题带来很大的方便.
本题难度:一般
2、选择题 如图所示,固定在地面上的半圆轨道直径ab水平,质点P从a点正上方高H处自由下落,经过轨道后从b点冲出竖直上抛,上升的最大高度为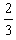 H,空气阻力不计。当质点原路返回再从轨道a点冲出时,能上升的最大高度h为
H,空气阻力不计。当质点原路返回再从轨道a点冲出时,能上升的最大高度h为

[? ]
A.h= H
H
B.h=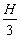
C.h<
D. <h<
<h< H
H
参考答案:D
本题解析:
本题难度:一般
3、选择题 不同质量的两个物体由同一地点以相同的动能竖直向上抛出,不计空气阻力,则这两个物体(?)
A.所能达到的最大高度和最大重力势能都相同
B.所能达到的最大高度不同,但最大重力势能相同
C.所能达到的最大高度和最大重力势能均不同
D.所能达到的最大高度相同,但最大重力势能不同
参考答案:B
本题解析:由动能定理知,-mgh=0-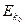 ,由于m不同,Ek相同,故h不同,但Ep=mgh=
,由于m不同,Ek相同,故h不同,但Ep=mgh=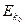 ,故Ep相同.
,故Ep相同.
本题难度:简单
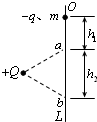
4、选择题 如图所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点由静止释放后,通过a的速率为
.则下列说法正确的是( )
A.小环通过b点的速率为
B.小环从O到b,电场力做的功可能为零
C.小环在Oa之间的速度是先增大后减小
D.小环在ab之间的速度是先减小后增大