1、简答题  如图所示，在一光滑的水平面上有两块高度相同的木板B和C，C的右端固定一轻质弹簧，重物A（视为质点）位于B的右端．A、B、C的质量均为m．现A和B以同一速度v0滑向静止的C，B和C发生正碰．碰后B和C粘在一起运动，A在C上滑行，与弹簧相碰后返回，恰好停在木板C的左端．试求：
（1）A停在木板C的左端后A、B、C共同运动的速度v；
（2）整个过程中系统克服摩擦力做功而产生的内能W；
（3）若重物A与木板C间的动摩擦因数为μ，求重物A对木板C相对位移的最大值sm及系统的最大弹性势能Epm．

参考答案：（1）A、B、C三个物体组成的系统动量守恒，设达到的共同运动速度为v，则：
2mv0=3mv
解得：v=23v0
（2）B和C发生正碰，B和C组成的系统在碰撞前后动量守恒，设B和C粘在一起运动的速度为v1，则：
? mv0=2mv1
解得：v1=12v0
设整个过程系统克服摩擦力做功而产生的内能为W，则：
?W=12mv20+122mv21-123mv2=112mv20
（3）重物从左向右相对木板C的位移由零到最大过程中，克服摩擦力做功而产生的内能为全程产生内能W的一半．
设相对位移的最大值为sm，则：fsm=12W?
而：f=μmg?
故：sm=W2f=v2024mg
弹簧压缩到最短时，弹簧的弹性势能（即系统的弹性势能）为最大值Epm，此时三者速度相同，也为v=23v0，由能量守恒定律得：
EPm=12mv20+122mv21-123mv2-12W=124mv20
答：（1）A停在木板C的左端后A、B、C共同运动的速度v=23v0；
（2）整个过程中系统克服摩擦力做功而产生的内能W=112mv20；
（3）若重物A与木板C间的动摩擦因数为μ，求重物A对木板C相对位移的最大值sm及系统的最大弹性势能为124mv20．

本题解析：

本题难度：一般

2、简答题  如图所示光滑水平直轨道上有三个滑块A、B、C质量分别为mA=mC=2m和mB=m，A、B用细绳相连，中间有一压缩的弹簧（弹簧与滑块不栓接），开始时A、B以共同速度V0向右运动，C静止，某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三者的速度恰好相同．

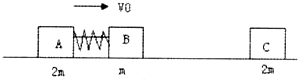
求：（1）B与C碰撞前B的速度
（2）弹簧释放的弹性势能多大．

参考答案：（1）设三者最后的共同速度为v共，由动量守恒得：
（mA+mB）v0=mAv共+mBvB
mBvB=（mB+mC）v共
三者动量守恒得：（2m+m）v0=（2m+m+2m）v共
得v共=35v0?所以vB=95v0
（2）弹簧释放的弹性势能
△Ep=122m(35v0)2+12m(95v0)2-123mv02=1235mv02．
答：（1）B与C碰撞前B的速度为95v0．
（2）弹簧释放的弹性势能为1235mv02．

本题解析：

本题难度：一般

3、计算题  如图所示，在光滑水平面上有木块A和B，mA=0.5kg，mB=0.4kg，它们的上表面是粗糙的，今有一小铁块C，mC=0.1kg，以初速v0=20m/s沿两木块表面滑过，最后停留在B上，此时B、C以共同速度v=3m/s运动，求：（1）A运动的速度vA=？
（2）小铁块C刚离开A时的速度vC′=?

参考答案：（1）vA=1m/s（2）vC′="11" m/s

本题解析：（1）对ABC由动量守恒得? mCv0=mAvA+（mB+mC）v?①
上式带入数据得? vA=1m/s?②
（2）当C刚离开A时AB有共同的速度vA，所以由动量守恒得
mCv0=（mA+mB）vA+mC vC′?③
上式带入数据得? vC′="11" m/s?④
点评：基础题，关键是判断在各个过程中谁和谁组成的系统动量守恒，然后列式求解

本题难度：一般

4、计算题  在光滑的水平面上，质量为m1的小球A以速率v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态，如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇，PQ＝1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的，求两小球质量之比m1/m2。

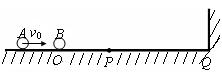
参考答案：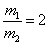

本题解析：解：从两小球碰撞后到它们再次相遇，小球A和B的速度大小保持不变，根据它们通过的路程，可知小球B和小球A在碰撞后的速度大小之比为4∶1。
设碰撞后小球A和B的速度分别为v1和v2，在碰撞过程中动量守恒，碰撞前后动量相等
?①
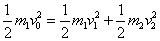?②
利用v2/v1=4，可解出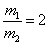?③

本题难度：一般

5、简答题  如图所示，甲、乙两小孩各坐一辆冰车在摩擦不计的冰面上相向运动，已知甲连同冰车的总质量M=30kg，乙连同冰车的总质量也是M=30kg，甲还推着一只质量m=15kg的箱子．甲、乙滑行的速度大小均为2m/s，为了避免相撞，在某时刻甲将箱子沿冰面推给乙，箱子滑到乙处时被乙接住．试求:①甲至少用多大的速度(相对于地面)将箱子推出，才可避免和乙相撞?②甲在推出时对箱子做了多少功?

参考答案：①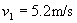②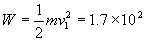

本题解析：甲推出箱子可使自己减速，而乙接住箱子，也可使其自己减速，甚至反向运动．若甲、乙刚好不相撞，条件应是在乙接住箱子后，甲、乙(包括箱子)的速度相同．根据动量守恒定律，我们先做定性分析:选甲、乙、箱子为系统，由于甲推出箱子前，系统的总动量的方向与甲的运动方向相同，所以在达到共同速 度时，系统的总动量方向应不变，故判断共同速度的方向在甲的原运动方向上．设:甲推出箱子前的运动方向为正方向，甲、乙初速度大小为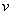，甲、乙、箱子后来的共同速度为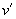，根据动量守律:
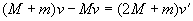，可求出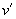=0.4m/s；再以甲与箱子为研究对象，甲推出箱子的过程中动量守恒，设箱子被推出后的速度为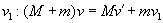，可求出被推出后箱子的速度为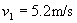.由动能定理，甲推出箱子的过程对箱子做功等于箱子动能的增加量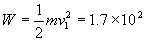J．
在本题中，对甲、乙不相撞的条件的分析，是解决问题的关键．而在具体的求解过程中，如何选择研究对象和过程始末去运用动量守恒定律，可以有不同的方式，例如，先选甲和箱子为系统，再选箱子和乙为系统也可解出，但要麻烦一些，不妨试一试，作一比较．

本题难度：简单