1、计算题  如图，在区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t=0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内。已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上点离开磁场。求：
（1）粒子在磁场中做圆周运动的半径R及粒子的比荷q/m；
（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；
（3）从粒子发射到全部粒子离开磁场所用的时间。

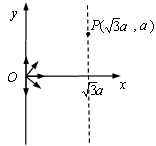
参考答案：解：（1）初速度沿y轴的正方向的粒子在磁场中的运动轨迹如图1所示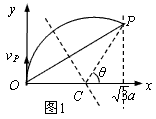：粒子沿y轴的正方向进入磁场，从P点经过，作OP的垂直平分线与x轴的交点为圆心C，在直角三角形中有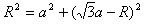
解得，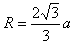
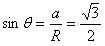
则粒子做圆周运动的的圆心角为120°，周期为T=3t0
粒子做圆周运动的向心力由洛仑兹力提供，根据牛顿第二定律得，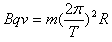
化简得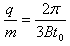
（2）依题意，同一时刻仍在磁场内的粒子到O点距离相同。在t0时刻仍在磁场内的粒子应位于以O为圆心、OP为半径的弧MN上，如图2所示：设此时位于P、M、N三点的粒子的初速度分别为vP、vM、vN。由对称性可知：vP与OP、vM与OM、vN与ON的夹角均为60°，设vM、vN与y轴的夹角分别为θM、θN，由几何关系有：θM=60°，θN=120°
对于所有此时刻仍在磁场内的粒子，其初速度与y轴的正方向的夹角范围应满足60°≤θ≤120°
（3）在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切，其轨迹如图3所示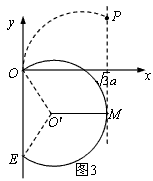：在三角形OO"E中，两个相等的腰为
而它的高是
半径O"E与y轴的的夹角是30°，这种粒子的圆心角是240°，所用时间为2t0
所以从粒子发射到全部离开所用时间为2t0

本题解析：

本题难度：困难

2、选择题  如图所示，在垂直纸面向里的匀强磁场的边界上，有两个质量和电荷量均相等的正、负离子（不计重力），从O点以相同的速度υ0先后射入磁场中，入射方向与边界夹角为θ，则正、负离子在磁场中

[? ]
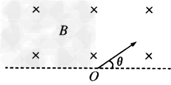
A．运动轨迹的半径相同
B．运动时间相同
C．重新回到边界时速度的大小和方向相同
D．重新回到边界的位置与O点的距离不相等

参考答案：AC

本题解析：

本题难度：一般

3、填空题  B．有一束粒子，以同一速度飞入匀强磁场中，在磁场中它们的轨迹分别为如右图中的a、b、c所示，已知磁场方向与速度方向垂直并垂直纸面向里，从这些轨迹能得出轨迹a的粒子带______电，轨迹c的粒子带______电．

参考答案：三种粒子的初速度方向相同，均向右；
a向上偏转，b不偏转，c向下偏转，说明粒子a受洛伦兹力向上，b不受洛仑兹力，c受向下的洛伦兹力；
根据左手定则可以判断a带正电，b不带电，c带负电；
故答案为：正，负

本题解析：

本题难度：一般

4、填空题  如图示，一个质子以速度v进入匀强磁场中，速度方向与磁场方向垂直．匀强磁场的磁感强度为B，质子的电荷为q，质量为m．质子在洛伦兹力的作用下做匀速圆周运动，用所给的这些物理量，推导出质子在磁场中做圆周运动的半径R的表达式为______．已知磁场的磁感强度B=6.3×10-2T，质子电荷q=1.6×10-19C，质子质量m=1.7×10-27kg，则计算出质子做圆周运动的周期为______s（保留二位有效数字）．

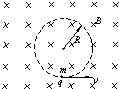
参考答案：带电粒子在匀强磁场中运动时，洛伦兹力提供向心力，即：qvB=mv2R，所以：R=mvqB
又：vT=2πR，所以T=2πmqB，
代人数据得：T=2πmqB=2×3.14×1.7×10-271.6×1019×6.3×10-2s=1.1×10-6s
故答案为：R=mvqB；1.1×10-6

本题解析：

本题难度：一般

5、选择题  
A．速率一定越小
B．速率一定越大
C．在磁场中通过的路程越长
D．在磁场中的周期一定越大