1、填空题  如图所示，在光滑水平地面上，有两个光滑的直角三形木块A和B，底边长分别为a、b，质量分别为M、m，若M = 4m，且不计任何摩擦力，当B滑到底部时，A向后移了?距离？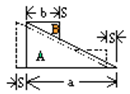

参考答案：（a-b）/5

本题解析：此题为人船模型问题，AB两木块水平方向动量守恒，设A向后移动的距离为x，则B向前移动距离为a-b-x，所以有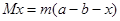，解得
故答案为：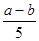

本题难度：简单

2、计算题  如图所示，人站在小车上推着木箱，一起在光滑水平冰面上以速度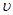运动，小车与木箱质量均为m，人的质量为2m，突然发现正前方有一冰窟窿，为防止人掉入窟窿，人用力向右推木箱，推出木箱后，人和车以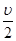的速度仍向前运动，为避开危险，人向后跳车.求：

①人推开木箱时木箱对地的速度多大；
②人跳车后车对地的最小速度.

参考答案：①2.5v?②1.5v

本题解析：取向右为正方向，根据动量守恒定律有推出木箱的过程：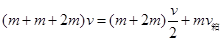
人跳车过程：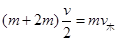
解得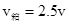

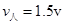
本题难度：一般

3、选择题  矩形滑块由不同材料的上下两层粘结在一起组成，将其放在光滑的水平面上，如图所示。质量为m的子弹以速度v水平射向滑块，若射击上层，则子弹恰好不射出；若射击下层，则子弹整个儿恰好嵌入，则上述两种情况相比较（?）

A．两次子弹对滑块做的功一样多
B．两次滑块所受冲量一样大
C．子弹嵌入下层过程中，系统产生的热量较多
D．子弹击中上层过程中，系统产生的热量较多

参考答案：AB

本题解析：考查依题意，设滑块的质量为M，对于子弹和滑块组成的系统，由动量守恒定律： ，解得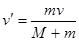：，即子弹最终与滑块有相同的速度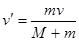；对滑块：（1）使用动能定理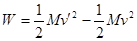：，由于v、相同，W相同，即两次子弹对滑块做的功一样多，A正确；（2）使用动量定理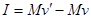：，由于v、相同，冲量I相同，即两次滑块所受冲量一样大，B正确；对系统：由能量守恒定律，系统产生的热量等于系统动能的减少量，即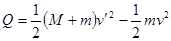，由于v、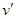相同，Q相同，CD错误；故选AB
点评：本题难度较小，注意灵活选择研究对象，产生的热量Q只与相对位移有关

本题难度：一般

4、简答题  如图所示，甲车的质量是2kg，静止在光滑水平面上，上表面光滑，右端放一个质量为1kg的小物体．乙车质量为4kg，以5m/s的速度向左运动，与甲车碰撞以后甲车获得8m/s的速度，物体滑到乙车上．若乙车足够长，上表面与物体的动摩擦因数为0.2，来源:91考试网 91eXAm.org则物体在乙车上表面滑行多长时间相对乙车静止？（g取10m/s2）

参考答案：乙与甲碰撞动量守恒：?
m乙v乙=m乙v乙′+m甲v甲′?
小物体m在乙上滑动至有共同速度v，对小物体与乙车运用动量守恒定律得?
m乙v乙′=（m+m乙）v?
对小物体应用牛顿第二定律得a=μg?
所以t=vμg?
代入数据得t=0.4s?
答：物体在乙车上表面滑行0.4s时间相对乙车静止．

本题解析：

本题难度：一般

5、计算题  如图10所示，光滑水平面上有一长板车，车的上表面OA段是一长为L的水平粗糙轨道，A的右侧光滑，水平轨道左侧是一光滑斜面轨道，斜面轨道与水平轨道在O点平滑连接．车右端固定一个处于锁定状态的压缩轻弹簧，其弹性势能为Ep，一质量为m的小物体(可视为质点)紧靠弹簧，小物体与粗糙水平轨道间的动摩擦因数为μ，整个装置处于静止状态．现将轻弹簧解除锁定，小物体被弹出后滑上水平粗糙轨道．车的质量为 2m，斜面轨道的长度足够长，忽略小物体运动经过O点处产生的机械能损失，不计空气阻力．求：
（1）解除锁定结束后小物体获得的最大动能；
（2）当μ满足什么条件小物体能滑到斜面轨道上，满足此条件时小物体能上升的最大高度为多少?

参考答案：（1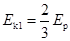）（2）

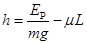
本题解析：本题考查系统动量守恒，根据系统受力情况分析出在解锁弹开后动量守恒，因为小车表面粗糙系统的机械能不守恒
(1)、设解锁弹开后小物体的最大速度饷大小为v1，小物体的最大动啦为Ek? ,此时长板车的速度大小为v2，研究解锁弹开过程小物体和车组成的系统，根据动量守恒和机械能守恒，
有 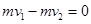?①?（2分）
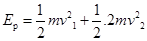?②?（2分）
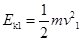?③（2分）
联立①②③式解得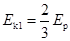．（2分）
(2)、小物体相对车静止时，二者有共同的速度设为v共，
长板车和小物体组成的系统水平方向动量守恒 ：
?④?（2分）
所以v共=0?
要使小物体能滑上斜面轨道，必须满足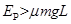（2分）
即当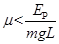时，小物体能滑上斜面轨道?
设小物体上升的最大高度为h，此瞬间小物体相对车静止，由④式知两者有共同速度为零．
根据系统能量守恒有?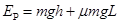?（2分）
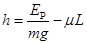解得：．（2分）

本题难度：一般