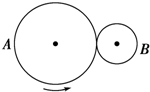
1、填空题  如图1—12所示， A、B两轮半径之比为1 ：3，两轮边缘挤压在一起，在两轮转动时，接触点不存在打滑的现象，则两轮边缘的线速度大小之比等于         ，两轮的转速之比等于        ，A轮半径中点与B轮边缘的角速度大小之比等于          。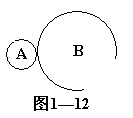

参考答案：1 ：1，3 ：1，3 ：1。

本题解析：接触点不打滑，则两轮线速度相同。据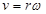，可知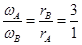，两轮的转速之比等于角速度之比。

本题难度：一般

2、简答题  如图所示为一实验小车中利用光脉冲测量车速和行程的装置的示意图，A为光源，B为光电接收器，A、B均固定在车身上，C为小车的车轮，D为与C同轴相连的齿轮．车轮转动时，A发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号，被B接收并转换成电信号，由电子电路记录和显示．若实验显示单位时间内的脉冲数为n，累计脉冲数为N，则要测出小车的速度和行程还必须测量的物理量或数据是______；小车速度的表达式为v=______；行程的表达式为s=______．

参考答案：因为B在单位时间内接到的脉冲数为n，每个间隙转动的时间t=1n，
设一周有P个齿，则有P个间隙，那么转动周期T=Pt=pn，
∴小车的线速度为：v=2πRT，联立各式得：v=2πRnP，所以要求车速必须测量出车轮的半径R和齿轮数P．
当脉冲总数为N时，则经过的时间t总=Nt=Nn，
所以小车的行程为：s=vt总=2πRNP．
故答案为：车轮半径R和齿轮的齿数P；
2πRnP；
2πRNP．

本题解析：

本题难度：一般

3、简答题  某物体做匀速圆周运动，其运动半径为2m，如该物体至运动中心的连线在2s内扫过的圆心角为540°，求：（1）该物体的运动周期；（2）转速；（3）角速度；（4）线速度．

参考答案：（1）由几何关系，2s内转过的角度θ=540°
所以ω=θt=34πrad/s
T=2πω=83s
（2）转速n=1T=38r/s
（4）线速度v=Rω=1.5m/s
答：（1）该物体的运动周期为83s；（2）转速为38r/s；（3）角速度为34πrad/s；（4）线速度为1.5m/s．

本题解析：

本题难度：一般

4、选择题  如图所示，一个小球沿竖直放置的光滑圆环形轨道做圆周运动，关于小球的运动情况，下列说法中正确的是（　　）
A．小球的线速度方向时刻在变化，但总沿圆周切线方向
B．小球的加速度方向时刻在变化，但总是指向圆心的
C．小球的线速度大小保持不变
D．小球的加速度大小保持不变