|
高考物理知识大全《动能定理及应用》高频试题预测(2019年最新版)(八)
2019-03-15 17:47:45
【 大 中 小】
|
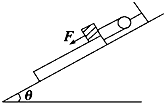
1、选择题 如图所示,在倾角为θ的光滑斜面上,一根细绳通过定滑轮分别与木板、小滑块(可视为质点)相连,小滑块质量为m,木板质量为M,木板长为L,小滑块与木板间的动摩擦因数为μ,开始时小滑块静止在木板的上端,现用与斜面平行的拉力F将小滑块缓慢拉至木板的下端,则在此过程中( )
A.拉力F的大小为mgμcosθ+(M-m)gsinθ
B.拉力F的大小为2mgμcosθ+(M-m)gsinθ
C.拉力F做的功为mgμLcosθ+(M-m)gLsinθ
D.拉力F做的功为mgμLcosθ+ (M-m)gsinθ
| 
参考答案:
A、B对木板:设细绳的拉力大小为T.根据平衡条件得:T=Mgsinθ+μmgcosθ
? 对小滑块:由平衡条件得:F+mgcosθ=T+μmgcosθ
联立上两式得:F=2mgμcosθ+(M-m)gsinθ? 故A错误,B正确.
C、DF是恒力,将小滑块缓慢拉至木板的下端过程中,滑块相对地的位移大小为L2,则拉力F做的功为W=F?L2=mgμLcosθ+L2(M-m)gsinθ.故C错误,D正确.
故选BD
本题解析:
本题难度:简单
2、简答题 在距离地面10m高处,以10m/s的速度抛出一质量为1kg的物体,已知物体落地时的速度为16m/s,求:(取g=10m/s2)
(1)抛出时人对物体做的功时多少?
(2)飞行过程中物体克服阻力做的功是多少?
参考答案:(1)由动能定理可知人抛物体对物体做的功等于物体获得的初动能W=12mv2=12×1?×102J=50J
? (2)设克服阻力做的功为Wf,则由动能定理得:
? ? WG-Wf=12mv2-12mv20
? ?解得:Wf=1×10×10-12×1×162+12×?1×102=22J
答:(1)抛出时人对物体做的功为50J;(2)飞行过程中物体克服阻力做的功为22J.
本题解析:
本题难度:一般
3、计算题 如图所示,在长为L的轻杆中点A和端点B各固定一质量均为m的小球,杆可绕无摩擦的轴O转动,使杆从水平位置无初速释放摆下。求当杆转到竖直位置时,轻杆对A、B两球分别做了多少功?
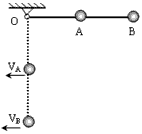
参考答案:解:若取B的最低点为零重力势能参考平面,可得: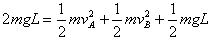 ① ①
又因A球对B球在各个时刻对应的角速度相同,故 ② ②
由①②式得:
根据动能定理,可解出杆对A、B做的功
对于A有: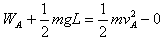 ,即: ,即:
对于B有: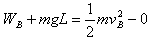 ,即: ,即: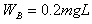
本题解析:
本题难度:困难
4、简答题 如图a所示,水平桌面的左端固定一个竖直放置的光滑圆弧轨道,圆弧轨道底端与水平桌面相切C点,桌面CD长L=1m,高h2=0.5m,有质量为m(m为末知)的小物块从圆弧上A点由静止释放,A点距桌面的高度h1=0.2m,小物块经过圆弧轨道底端滑到桌面CD上,在桌面CD上运动时始终受到一个水平向右的恒力F作用.然后从D点飞出做平抛运动,最后落到水平地面上.设小物块从D点飞落到的水平地面上的水平距离为x,如图b是x2-F的图象,取重力加速度g=10m/s2.
(1)试写出小物块经D点时的速度vD与x的关系表达式;
(2)小物体与水平桌面CD间动摩擦因数μ是多大?
(3)若小物体与水平桌面CD间动摩擦因数μ是从第(2)问中的μ值的一半,再将小物块从A由静止释放,经过D点滑出后的水平位移大小为1m,求此情况下的恒力F的大小?
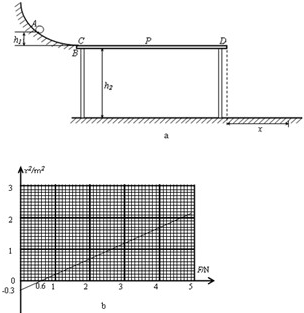
参考答案:(1)物体从D滑出后做平抛运动,
水平方向x=vDt,竖直方向:h2=12gt2,
解得vD=x
本题解析:
本题难度:一般
5、简答题 在半径为R=12000km的某星球表面,宇航员做了如下实验,实验装置如图.竖直面内的光滑轨道有轨道AB和圆轨道BC组成,将质量为m=0.1kg的小球,从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点是对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙,求:
(1)圆轨道的半径;
(2)该星球表面的重力加速度大小;
(3)该星球的第一宇宙速度.

参考答案:(1)小球过C点时,由牛顿第二定律得:
F+mg=mv2Cr2,
由动能定理有:
mg(H-2r)=12mvC2-0,
联立解得:F=2mgrH-5mg,
由图可知:H1=1m时,F1=0,
即:0=2mgr×0.5-5mg,
解得轨道半径为:r=0.4m;
(2)由图象得:H2=2m时,F2=6N,
即:6=2×0.1×g0.4×2-5×0.1×g,
解得:g=12m/s2;
(3)由牛顿第二定律得:
mv2R=mg,
第一宇宙速度为:v=
本题解析:
本题难度:一般
| 