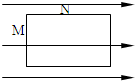
1、选择题  如图所示，在匀强磁场中，MN、PQ是两条平行金属导轨，而ab、cd为串有电压表和电流表的两根金属棒，两只电表可看成理想电表当两棒以相同速度向右匀速运动时（运动过程中两棒始终与导轨接触）

[? ]
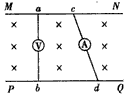
A．电压表有读数，电流表有读数
B．电压表无读数，电流表无读数
C．电压表有读数，电流表无读数
D．电压表无读数，电流表有读数

参考答案：B

本题解析：

本题难度：简单

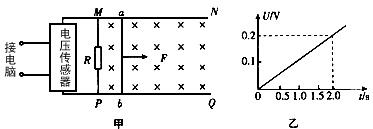
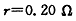2、计算题  如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.30m，导轨电阻忽略不计，其间连接有固定电阻导轨上停放一质量m=0.10kg，电阻的金属杆ab，整个装置处于磁感应强度B=0.50T的匀强磁场中，磁场方向竖直向下。用一外力F沿水平方向拉金属杆ab，使之由静止开始运动，电压传感器可将R两端的电压U即时采集并输入电脑，获得电压U随时间t变化的关系如图乙所示。
（1）利用上述条件证明金属杆做匀加速直线运动，并计算加速度的大小；
（2）求第2s末外力F的瞬时功率；
（3）如果水平外力从静止开始拉动杆2s所做的功W=0.35J，求金属杆上产生的焦耳热。

参考答案：解：（1）设路端电压为U，金属杆的运动速度为v，则感应电动势E= BLv
通过电阻R的电流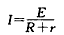
电阻R两端的电压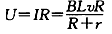
由图乙可得U=kt，k=0.10V/s，解得：
因为速度与时间成正比，所以金属杆做匀加速运动，加速度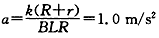（用其他方法证明也可以）
（2）在2s末，速度v2=at=2.0m/s
电动势E= BLv2 通过金属杆的电流
金属杆受安培力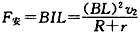
解得：F安=7.5×10-2N
设2s末外力大小为F2，由牛顿第二定律得F2- F安=ma
解得：F2=1.75×10-lN
故2s末时F的瞬时功率P=F2v2=0.35W。
（3）设回路产生的焦耳热为Q，由能量守恒定律得
解得：Q=0.15J 电阻R与金属杆的电阻r串联，产生焦耳热与电阻成正比，所以，
运用合比定理而
故在金属杆上产生的焦耳热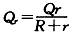
解得：Qr=5.0×10-2J。

本题解析：

本题难度：困难

3、选择题  如图，在光滑水平面上，有一竖直向下的匀强磁场，分布在宽为a的区域内，现有一边长为L（a＞L）的正方形闭和线框以垂直于磁场边界的初速度v0滑过磁场，线框刚好能穿过磁场。则线框在滑进磁场过程中产生的热量Q1与滑出磁场过程产生的热量Q2之比为

[? ]
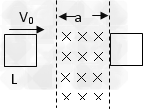
A、1：1?
B、2：1
C、3：1?
D、4：1

参考答案：C

本题解析：

本题难度：一般

4、选择题  如图所示，线框由A位置开始下落，在磁场中受到的安培力如果总小于重力，则它在A、B、C、D四个位置(B、D位置恰好线框有一半在磁场中)时，加速度关系为(? )

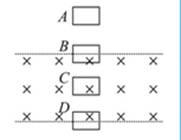
A.aA＞aB＞aC＞aD? B.aA＝aC＞aB＞aD
C.aA＝aC＞aD＞aB? D.aA＝aC＞aB＝aD

参考答案：选B.

本题解析：线框在A、C位置时只受重力作用，加速度aA＝aC＝g.线框在B、D位置时均受两个力的作用，其中安培力向上、重力向下.由于重力大于安培力，所以加速度向下，大小为a＝g－ F/m＜g.又线框在D点时速度大于B点速度，即FD＞FB，所以aD＜aB.因此加速度的关系为aA＝aC＞aB＞aD.选项B正确.

本题难度：一般

5、选择题  如图所示，将一线圈放在一匀强磁场中，线圈平面平行于磁感线，则线圈中有感应电流产生的是（ ? ）
A．当线圈绕N边转动
B．当线圈绕M边转动
C．将线圈垂直纸面向外运动
D．将线圈平行纸面向右运动