1、选择题 为了诊断病人的心脏功能和动脉血液黏稠情况,需测量血管中血液的流量,如图所示为电磁流量计示意图,将血管置于磁感应强度为B的磁场中,测得血管两侧a、b两点间电压为u,已知血管的直径为d,则血管中血液的流量Q(单位时间内流过的体积)为

[? ]
A.?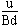 ?
?
B. 
C.? ?
?
D. 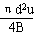
参考答案:C
本题解析:
本题难度:一般
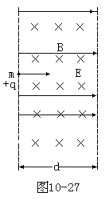
2、简答题 图10-27为方向相互垂直的匀强电场和匀强磁场区域。电场强度为E,磁感强度为B,复合场的水平宽度为d,竖直方向足够长。现有一束电量为+q、质量为m初速度各不相同的粒子沿电场方向进入场区,求能逸出场区的粒子的动能增量ΔEk。
参考答案:ΔEk=0
本题解析:由于带电粒子在磁场中受到洛仑兹力是与粒子运动方向垂直的。它只能使速度方向发生变。粒子速度越大,方向变化越快。因此当一束初速度不同、电量为+q、质量为m的带电粒子射入电场中,将发生不同程度的偏转。有些粒子虽发生偏转,但仍能从入射界面的对面逸出场区(同错解答案);有些粒子将留在场区内运动;有些粒子将折回入射面并从入射面逸出场区。由于洛仑兹力不会使粒子速度大小发生变化,故逸出场区的粒子的动能增量等于电场力功。对于那些折回入射面的粒子电场力功为零,其动能不变,动能增量ΔEk=0。
本题难度:一般
3、简答题 如图1所示,A、B两块金属板水平放置,相距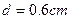 ,两板间加有一周期性变化的电压,当B板接地时,A板电势
,两板间加有一周期性变化的电压,当B板接地时,A板电势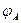 随时间t变化的情况如图2所示。在两板间的电场中,将一带负电的粒子从B板中央处由静止释放,若该带电粒子受到的电场力为重力的两倍,要使该粒子能够达到A板,交变电压的周期至少为多大。(g取
随时间t变化的情况如图2所示。在两板间的电场中,将一带负电的粒子从B板中央处由静止释放,若该带电粒子受到的电场力为重力的两倍,要使该粒子能够达到A板,交变电压的周期至少为多大。(g取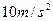 )
)
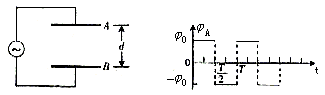
图1?图2
参考答案: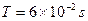
本题解析:设电场力为F,则 ,得
,得
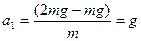
前半周期上升高度: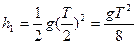 ,后半周期先减速上升,后加速下降,其加速度:
,后半周期先减速上升,后加速下降,其加速度:
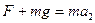 得
得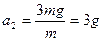
减速时间为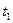 则
则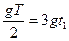 ,
,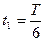
此段时间内上升高度:
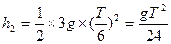
则上升的总高度: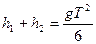
后半周期的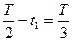 时间内,粒子向下加速运动,下降的高度:
时间内,粒子向下加速运动,下降的高度:

上述计算说明,在一个周期内上升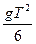 ,再回落
,再回落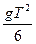 ,且具有向下的速度。
,且具有向下的速度。
如果周期小,粒子不能到达A板。设周期为T,上升的高度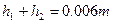 则:
则:
 ,
,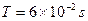 。
。
本题难度:简单
4、简答题 . 如图,在宽度分别为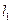 和
和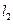 的两个毗邻的条形区域分别有匀强磁场和匀强电场,磁场方向垂直于纸面向里,电场方向与电、磁场分界线平行向右。一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场,然后以垂直于电、磁场分界线的方向进入电场,最后从电场边界上的Q点射出。已知PQ垂直于电场方向,粒子轨迹与电、磁场分界线的交点到PQ的距离为d。不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比。
的两个毗邻的条形区域分别有匀强磁场和匀强电场,磁场方向垂直于纸面向里,电场方向与电、磁场分界线平行向右。一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场,然后以垂直于电、磁场分界线的方向进入电场,最后从电场边界上的Q点射出。已知PQ垂直于电场方向,粒子轨迹与电、磁场分界线的交点到PQ的距离为d。不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比。



参考答案: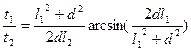
本题解析:本题考查带电粒子在有界磁场中的运动.

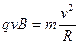
 粒子在磁场中做匀速圆周运动,如图所示.由于粒子在分界线处的速度与分界线垂直,圆心O应在分界线上,OP长度即为粒子运动的圆弧的半径R.由几何关系得
粒子在磁场中做匀速圆周运动,如图所示.由于粒子在分界线处的速度与分界线垂直,圆心O应在分界线上,OP长度即为粒子运动的圆弧的半径R.由几何关系得

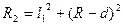 ………①
………①
 设粒子的质量和所带正电荷分别为m和q,由洛伦兹力公式和牛顿第二定律得
设粒子的质量和所带正电荷分别为m和q,由洛伦兹力公式和牛顿第二定律得

 ……………②
……………②

 设
设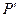 为虚线与分界线的交点,
为虚线与分界线的交点,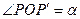 ,则粒子在磁场中的运动时间为
,则粒子在磁场中的运动时间为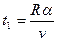 ……③
……③
 式中有
式中有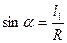 ………④粒子进入电场后做类平抛运动,其初速度为v,方向垂直于电场.设粒子的加速度大小为a,由牛顿第二定律得
………④粒子进入电场后做类平抛运动,其初速度为v,方向垂直于电场.设粒子的加速度大小为a,由牛顿第二定律得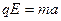 …………⑤
…………⑤
 由运动学公式有
由运动学公式有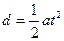 ……⑥?
……⑥?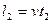 ………⑦
………⑦
 由①②⑤⑥⑦式得
由①②⑤⑥⑦式得 …………⑧
…………⑧
 由①③④⑦式得
由①③④⑦式得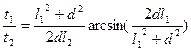
本题难度:简单
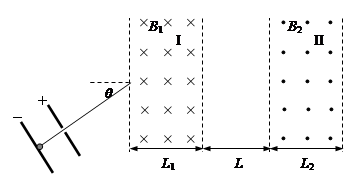
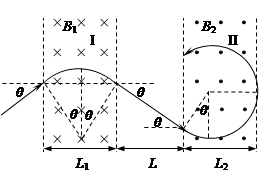
5、计算题 扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆,其简化模型如图所示:I、II两处的条形匀强磁场区域的宽度分别为L1、L2,边界竖直,I区域的右边界和II区域的左边界相距L,磁感应强度大小分别为B1、B2,方向相反且垂直纸面。一质量为m、电量为-q、重力不计的粒子,从靠近平行板电容器的负极板处由静止释放,两极板间电压为U,粒子经电场加速后平行纸面射入I区域,射入时的速度方向与水平方向的夹角θ=30°。
(1)当L1=L,B1=B0时,粒子从I区域右边界射出时速度与水平方向的夹角也为30°,求B0及粒子在I区域中运动的时间t1;
(2)若L2=L1=L,B2=B1=B0,求粒子在I区域中的最高点与II区域中的最低点之间的高度差h;
(3)若L2=L1=L,B1=B0,为使粒子能返回I区域,求B2应满足的条件;
(4)若L1≠L2,B1≠B2,且已保证粒子能从II区域的右边界射出,为使粒子从II区域右边界射出时速度与从I区域左边界射入时的方向总相同,求B1、B2、L1、L2之间应满足的关系式。
参考答案:(1)t1= ?(2)h=h1+h2+h3=(2-
?(2)h=h1+h2+h3=(2-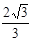 )L (3)B2≥
)L (3)B2≥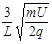 ?(4)B1L1=B2L2
?(4)B1L1=B2L2
本题解析:(1)在电场中,由动能定理有
qU=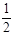 mv02-0?………………… ①(1分)
mv02-0?………………… ①(1分)
在磁场1区域中,粒子的运动轨迹如图1所示,

由几何关系有
L=2R0sinθ?……………………… ②(1分)
由牛顿第二定律有
qv0B0=m ?……………………… ③(1分)
?……………………… ③(1分)
由①②③解得:B0=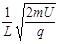 ?… ④(1分)
?… ④(1分)
由运动学规律有
R0·2θ=v0t1?……………………… ⑤(1分)
得:t1= ?…………… ⑥(1分)
?…………… ⑥(1分)
(2)粒子的运动轨迹如图2所示,

由几何关系有
h1=h3=R0-R0cosθ?…………… ⑦(2分)
h2=Ltanθ?………………………… ⑧(2分)
故所求高度差
h=h1+h2+h3=(2-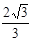 )L?…… ⑨(1分)
)L?…… ⑨(1分)
(3)粒子的运动轨迹如图3所示,
由几何关系有
L=R2+R2sinθ?………………… ⑩(2分)
由牛顿第二定律有
qv0B2=m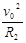 ?…………………… ⑾(1分)
?…………………… ⑾(1分)
由①⑩⑾解得:B2=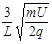 ?… ⑿(1分)
?… ⑿(1分)
所以满足条件为B2≥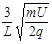 ?… ⒀(1分)
?… ⒀(1分)
(4)粒子的运动轨迹如图4所示,
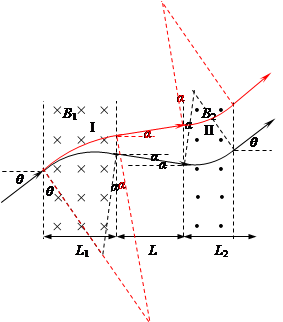
设粒子从I区域射出时与水平方向的夹角
为α,由几何关系有
L1=R1sinθ+R1sinα?………… ⒁(1分)
L2=R2sinθ+R2sinα?………… ⒂(1分)
或
L1=R1sinθ-R1sinα
L2=R2sinθ-R2sinα?
由牛顿第二定律有
qv0B1=m ?………………… ⒃(1分)
?………………… ⒃(1分)
qv0B2=m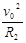 ?………………… ⒄(1分)
?………………… ⒄(1分)
由⒁⒂⒃⒄解得:B1L1=B2L2?… ⒅(2分)
本题考查带电粒子在有界磁场中的运动,难度较大,先根据电场力做功求得末速度,和几何关系求得半径,再由洛伦兹力提供向心力求得磁感强度大小,在两个磁场中由于磁场方向不同,偏转方向正好相反,先画出运动轨迹,再由几何关系求得半径大小,由洛伦兹力提供向心力列式求解
本题难度:一般