1、简答题  “绿色奥运”是2008年北京奥运会的三大理念之一，奥组委决定在各比赛场馆使用新型节能环保电动车，届时奥运会500名志愿者将担任司机，负责接送比赛选手和运输器材．在检测某款电动车性能的某次实验中，质量为800kg的电动车由静止开始沿平直公路行驶，达到的最大速度为15m/s，利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v，并描绘出F-

参考答案：（1）由图线分析可知，图线AB牵引力F不变，阻力f不变，电动车由静止开始做匀加速直线运动；图线BC的斜率表示汽车的功率P，P不变，达到额定功率后，则电动车所受牵引力逐渐减小做加速度减小的变加速直线运动，直至达最大速度15m/s；此后电动车作匀速直线运动
由图象可得，当最大速度vmax=15m/s时，牵引力为Fmin=400N
故恒定阻力f=Fmin=400N…①
额定功率P=Fminvmin=6kW…②
匀加速运动的末速度v=PF…③
代入数据解得v=3m/s
（2）匀加速运动的加速度a=F-fm=2000-400800…④
解得a=2m/s2…
（3）环保电动车在速度达到3m/s之前、一直做匀加速直线运动
故所求时间为t=v1a…⑤
将v1=2m．s代入上式解得t=1s
答：（1）电动车在A-B过程做匀加速直线运动，在B-C过程做加速度减小的变加速运动．电动车的额定功率为6000W．
（2）匀加速直线运动过程的加速度的大小是2m/s2．
（3）电动车由静止开始运动，经过1s时间速度达到2m/s．

本题解析：

本题难度：一般

2、选择题  质量为2m的物体A与水平面间的摩擦可以忽略不计，质量为m的物体B与地面的动摩擦因数为μ．A、B并排放置在水平面上，用在水平推力F的作用下，共同向右做加速运动．此时（　　）
A．A对B的推力可能小于μmg
B．若μ=0则A对B的推力等于零
C．B对A的推力可能小于

参考答案：设A对B的推力为N．
A、由题意，B向右加速运动，具有向右的加速度，B所受的滑动摩擦力大小为μmg，方向向左，则根据牛顿第二定律得知合外力向右，所以A对B的推力一定大于μmg．故A错误．
B、若μ=0，根据牛顿第二定律得：
对整体：a=F3m，
对B：A对B的推力N=ma=F3≠0．故B错误．
C、D对整体，则有：F-μmg=3ma，得F=μmg+3ma
对B；N-μmg=ma，得N=μmg+ma
若μ=0，联立解得，N=F3；若μ≠0，解得，N＞F3．故C错误，D正确．
故选D

本题解析：

本题难度：简单

3、简答题  在质量为M=1kg的小车上，竖直固定着一个质量为m=0.2kg，高h=0.05m、总电阻R=100Ω、n=100匝矩形线圈，且小车与线圈的水平长度l相同．现线圈和小车一起在光滑的水平面上运动，速度为v1=10m/s，随后穿过与线圈平面垂直，磁感应强度B=1.0T的水平有界匀强磁场，方向垂直纸面向里，如图（1）所示．已知小车运动（包括线圈）的速度v随车的位移s变化的v-s图象如图（2）所示．求：
（1）小车的水平长度l和磁场的宽度d
（2）小车的位移s=10cm时线圈中的电流大小I以及此时小车的加速度a
（3）线圈和小车通过磁场的过程中线圈电阻的发热量Q

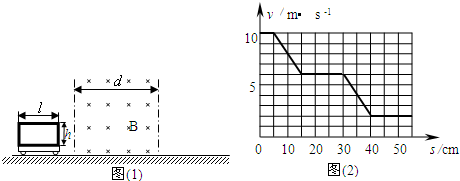
参考答案：（1）由图可知，从s=5cm开始，线圈进入磁场，线圈中有感应电流，受安培力作用，小车做减速运动，速度v随位移s减小，当s=15cm时，线圈完全进入磁场，线圈中感应电流消失，小车做匀速运动．因此小车的水平长度l=10cm．
当s=30cm时，线圈开始离开磁场，则d=（30-5）cm=25cm
（2）当s=10cm时，由图象中可知线圈右边切割磁感线的速度v2=8m/s
由闭合电路欧姆定律得线圈中的电流I=ER=nBhv2R
解得：I=100×1×0.05×8100A=0.4A
此时线圈所受安培力F=nBIh=100×1×0.4×0.05N=2N
小车的加速度a=F(M+m)=21.2m/s2=1.67m/s2
（3）由图象可知，线圈左边离开磁场时，小车的速度为v3=2m/s．
线圈进入磁场和离开磁场时，克服安培力做功，线卷的动能减少，转化成电能消耗在线圈上产生电热．Q=12(M+m)(v21-v23)
解得线圈电阻发热量Q=57.6J?
答：（1）小车的水平长度10cm和磁场的宽度25cm；
（2）小车的位移s=10cm时线圈中的电流大小I以及此时小车的加速度为1.67m/s2；
（3）线圈和小车通过磁场的过程中线圈电阻的发热量为57.6J．

本题解析：

本题难度：一般

4、计算题  如图所示，螺线管横截面积为S，线圈匝数为N，电阻为R1，管内有水平向左的变化磁场。螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内，与水平面的夹角为q，两导轨间距为L。导轨电阻忽略不计。导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中。金属杆ab垂直导轨，杆与导轨接触良好，并可沿导轨无摩擦滑动。已知金属杆ab的质量为m，电阻为R2，重力加速度为g。忽略螺线管磁场对金属杆ab的影响、忽略空气阻力。

（1）为使ab杆保持静止，求通过ab的电流的大小和方向；
（2）当ab杆保持静止时，求螺线管内磁场的磁感应强度B的变化率；
（3）若螺线管内方向向左的磁场的磁感应强度的变化率DB/Dt＝k（k＞0）。将金属杆ab由静止释放，杆将沿斜面向下运动。求当杆的速度为v时，杆的加速度大小。

参考答案：（1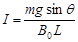），电流方向为由b到a（2）（3）

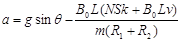
本题解析：（1）以金属杆ab为研究对象，根据平衡条件?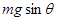- B0I L＝0（1分）
得 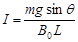?（1分）
通过ab杆电流方向为由b到a（或在图中标出）?（1分）
（2）根据法拉第电磁感应定律 （1分）
根据欧姆定律?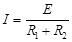?（1分）
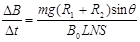得：?（1分）
（3）根据法拉第电磁感应定律?（1分）
ab杆切割磁感线产生的电动势 E2 ＝ B0Lv?（1分）
总电动势? E总 ＝ E1 + E2
感应电流?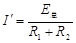?（1分）
根据牛顿第二定律?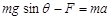?（1分）
安培力? F ＝ B0 I′L?（1分）
所以?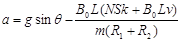?（1分）

本题难度：一般

5、简答题  一个质量m=10kg的静止物体与水平地面间滑动摩擦系数μ=0.5，受到一个大小为100N与水平方向成θ=37°的斜向上拉力作用而运动，假设拉力作用的时间为t=1s．（g取10m/s2．已知sin53°=0.8，cos53°=0.6）
（1）求1s内拉力做的功；
（2）求1s内摩擦力做的功；
（3）求1s内合外力做的功．

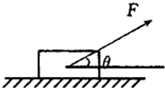
参考答案：（1）由受力分析
知：FN=G-Fsin37°=100-100×0.6=40N

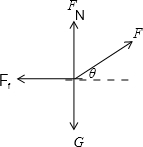
由摩擦力公式得：Ff=μFN=0.5×40=20N
由牛顿第二定律：F合=Fcos37°-Ff=ma
解得：a=6m/s2
由位移公式可得x=12at2=12×6×12=3m
故1s内拉力做的功：WF=Fxcos37°=100×3×0.8=240J
（2）WFf=Ffxcos180°=20×3×（-1）=-60J
（3）W合=F合x=max=10×6×3=180J
答：（1）1s内拉力做的功为240J；
（2）1s内摩擦力做的功为-60J；
（3）1s内合外力做的功为180J．

本题解析：

本题难度：一般