1、计算题  如图所示，光滑绝缘水平面AB与倾角θ=37°，长L=5m的绝缘斜面BC在B处圆滑相连，在斜面的C处有一与斜面垂直的弹性绝缘挡板，质量m=0.5kg、所带电荷量q=5×10-5C的绝缘带电小滑块（可看做质点）置于斜面的中点D，整个空间存在水平向右的匀强电场，场强E=2×l05N/C，现让滑块以v0=12m/s的速度沿斜面向上运动。设滑块与挡板碰撞前后所带电荷量不变、速度大小不变，滑块和斜面间的动摩擦因数μ=0.1，（g取10m/s2，sin37°=0.60，cos37°=0.8）求：

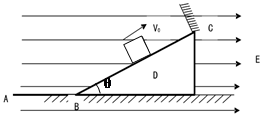
（1）滑块第一次与挡板碰撞时的速度大小；
（2）滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离；
（3）滑块运动的总路程。

参考答案：（1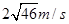）（2）1.6m（3）52.9m

本题解析：
试题分析:(1)设滑块第一次与挡板碰撞时的速度大小为V
静电力qE=10N，重力G=mg=5N。
摩擦力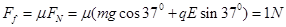
由动能定理：
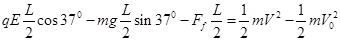
解得：
(2)设滑块第一次下滑到B端的速度为VB，滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离为x
由动能定理：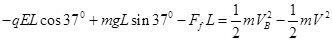
解得VB=8m/s
在水平面上滑行时，只有静电力做功，由动能定理：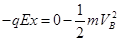
解得x=1.6m
(3) 设滑块第一次下滑到B端的动能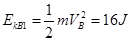，水平面光滑，从水平运动返回到B点，动能不变。
在斜面上往返一次克服摩擦力做功Wf=2FfL=10J
所以滑块还能滑到B点到达水平面一次，设在水平面上滑动的距离为x1
由动能定理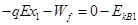：，解得 x1=0.6m
在水平面上滑动的总距离S1=2（x+x1）=4.4m
最后停在C点，在斜面上滑行的距离为S2
由动能定理：解得S2=48.5m
所以，滑块运动的总路程S=S1+S2=52.9m

本题难度：一般

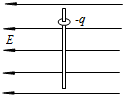
2、简答题  如图所示，在水平向左、电场强度为E的匀强电场中，竖直固定着一根足够长的粗糙绝缘杆，杆上套着一个质量为m、带有电荷量-q的小圆环，圆环与杆间的动摩擦因数为μ．
（1）由静止释放圆环，圆环沿杆下滑，求圆环下滑过程中受到的摩擦力f；
（2）若在匀强电场E的空间内再加上磁感应强度为B、方向垂直纸面向里的匀强磁场，圆环仍由静止开始沿杆下滑．求：
①圆环刚开始运动时加速度a0的大小；
②圆环下滑过程中的最大动能Ek．

参考答案：（1）在水平方向圆环受到的弹力N=qE
则摩擦力f=μN=μqE，方向竖直向上．
（2）①圆环刚开始运动时不受洛伦兹力，因此，摩擦力大小f=μqE
在竖直方向，由牛顿第二定律 mg-μqE=ma0
解得a0=mg-μqEm
②当重力与滑动摩擦力平衡时，圆环速度最大，动能最大．
即mg=μ（qvmB-qE）
最大速度vm=mg+μqEμqB
最大动能Ek=12mv2m=m(mg+μqE)22μ2q2B2
答：（1）由静止释放圆环，圆环沿杆下滑，圆环下滑过程中受到的摩擦力f=μqE；
（2）若在匀强电场E的空间内再加上磁感应强度为B、方向垂直纸面向里的匀强磁场，圆环仍由静止开始沿杆下滑，
①圆环刚开始运动时加速度大小为a0=mg-μqEm；
②圆环下滑过程中的最大动能Ek=m(mg+μqE)22μ2q2B2．

本题解析：

本题难度：一般

3、计算题  (2011年昆明模拟)如图甲所示，在倾角为30°的足够长光滑斜面AB前，有一粗糙水平面OA，OA长为4 m．有一质量为m的滑块，从O处由静止开始受一水平向右的力F作用．F按图乙所示的规律变化．滑块与OA间的动摩擦因数μ＝0.25，g取10 m/s2，试求：

(1)滑块到A处的速度大小；
(2)不计滑块在A处的速率变化，滑块冲上斜面AB的长度是多少？

参考答案：(1)5 ?m/s　(2)5 m

本题解析：(1)由题图乙知，在前2 m内，F1＝2mg，做正功；
在第3 m内，F2＝－0.5mg，做负功；
在第4 m内，F3＝0.
滑动摩擦力
Ff＝－μmg＝－0.25mg，始终做负功．
对OA过程由动能定理列式得
F1x1＋F2x2＋Ff·x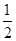＝?mv－0.
即2mg×2－0.5mg×1－0.25mg×4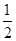＝?mv，
解得vA＝5 ?m/s.
(2)冲上斜面的过程，由动能定理得
－mg·L·sin30°＝0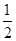－?mv，
所以冲上斜面AB的长度L＝5 m.

本题难度：一般

4、简答题  如图所示，V形细杆AOB能绕其对称轴OO′转到，OO′沿竖直方向，V形杆的两臂与转轴间的夹角均为α=45°．两质量均为m=0.1kg的小环，分别套在V形杆的两臂上，并用长为l=1.2m、能承受最大拉力Fmax=4.5N的轻质细线连结，环与臂间的最大静摩擦力等于两者间弹力的0.2倍．当杆以角速度ω转到时，细线始终处于水平状态，取g=10m/s2．
（1）求杆转动角速度ω的最小值；
（2）将杆的角速度从（1）问中求得的最小值开始缓慢增大，直到细线断裂，写出此过程中细线拉力随角速度变化的函数关系式；
（3）求第（2）问过程中杆对每个环所做的功．

参考答案：（1）∵角速度最小时，fmax沿杆向上，则
FNsin45°+fmaxcos45°=mg，
FNcos45°-fmaxsin45°=mrω12，
且fmax=0.2FN，r=l2，
代入数据解得ω1=103≈3.33rad/s
（2）当fmax沿杆向下时，有
FNsin45°=fmaxcos45°+mg，
FNcos45°+fmaxsin45°=mrω22，
代入数据解得ω2=5rad/s
当细线拉力刚达到最大时，有
FNsin45°=fmaxcos45°+mg，
FNcos45°+fmaxsin45°+Fmax=mrω32，
∴ω3=10rad/s
则F拉=

本题解析：

本题难度：一般

5、选择题  一半径为R的绝缘光滑圆环竖直放置在方向水平向右的、场强为E的匀强电场中，如图5所示，环上a，c是竖直直径的两端，b，d是水平直径的两端，质量为m的带电小球套在圆环上，并可沿环无摩擦滑动，已知小球自a点由静止释放，沿abc运动到d点时的速度恰好为零，由此可知（　　）
A．小球在d点时的加速度为零
B．小球在b点时的机械能最大
C．小球在d点时的电势能最小
D．小球在b点时的动能最大