1、选择题  如图所示，一个边长为2L的等腰直角三角形ABC区域内，有垂直纸面向里的匀强磁场，其左侧有一个用金属丝制成的边长为L的正方形线框abcd，线框以水平速度v匀速通过整个匀强磁场区域，设电流逆时针方向为正。则在线框通过磁场的过程中，线框中感应电流i随时间t变化的规律正确的是（    ）


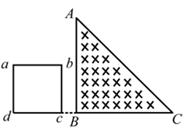
A.               B.               C.              D.

参考答案：A

本题解析：在0～t时间内，bc边进入磁场，切割有效长度不变，根据楞次定律可以判断电流逆时针，为正值，大小不变；在t～2t时间内ad边进入磁场，bc边开始穿出磁场，有效长度从零开始逐渐增大，感应电动势从零开始逐渐增大，电流从零开始逐渐增大，根据楞次定律可以判断电流顺时针，为负值；在2t～3t时间内ad边开始穿出磁场，有效长度从逐渐减小到零，感应电动势逐渐减小到零，电流逐渐减小到零，根据楞次定律可以判断电流顺时针，为负值，符合题意的图像是A图。
故选A
考点：法拉第电磁感应定律的应用
点评：本题关键点是弄清楚切割有效长度和电流的方向。

本题难度：困难

2、计算题  一个正方形导线圈边长a=0.2m，共有N=100匝，其总电阻r=4Ω，线圈与阻值R=16Ω的外电阻连成闭合回路，线圈所在区域存在着匀强磁场，磁场方向垂直线圈所在平面，如图甲所示，磁场的大小随时间变化如图乙所示，求：

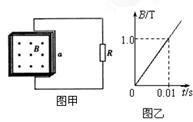
（1）线圈中产生的感应电动势大小。
（2）通过电阻R的电流大小。

参考答案：（1）（2）

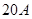
本题解析：（1）根据图乙，磁感应强度的变化率为：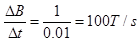
根据法拉第电磁感应定律，感应电动势为：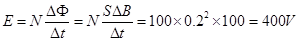
（2）根据闭合电路欧姆定律，电流为：
考点：考查了法拉第电磁感应定律，闭合回路欧姆定律

本题难度：一般

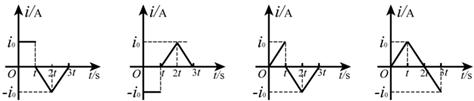
3、选择题  如图所示，宽度为l的有界匀强磁场的方向垂直纸面向里，磁感应强度的大小为B。闭合等腰直角三角形导线框abc位于纸面内，直角边ab水平且长为2l，线框总电阻为R。规定沿abca方向为感应电流的正方向。导线框以速度v匀速向右穿过磁场的过程中，感应电流随时间变化规律的图象是（   ）

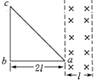
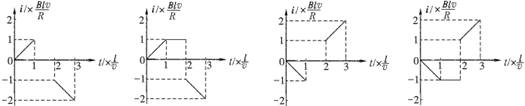
A                   B                   C                   D

参考答案：D

本题解析：由已知条件可知，在0-L/v时，感应电动势均匀增加，感应电流均匀增加，方向为顺时针，增加到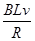；在L/v-2L/v时，磁通量无变化，感应电流为零，在2L/v-3L/v时，感应电流再均匀增加，不过是逆时针，故选D
考点：考查电磁感应与图像
点评：本题难度较小，感应电流的大小直接由切割磁感线的有效长度决定，方向由楞次定律判断即可

本题难度：一般

4、选择题  一矩形线圈位于一个方向垂直线圈平面向里的磁场中，如图a所示，磁感应强度B随t的变化规律如图b所示．以I表示线圈中的感应电流，以图a线圈上箭头所示方向的电流为正，则以下的i-t图中正确的是 （   ）

                                           

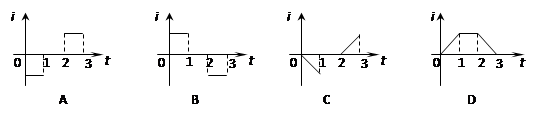
参考答案：A

本题解析：由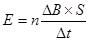可知在0-1s间电动势恒定，电流恒定，C错；在1-2s间磁通量不变，电流为零，D错；在0-1s间，磁通量增大，流过闭合线圈的感应电流逆时针，电流为负，由楞次定律可知在2-3s间电流方向顺时针，A对

本题难度：一般

5、计算题  如图甲所示，平行金属导轨竖直放置，导轨间距为L＝1m，上端接有电阻R1＝3Ω，下端接有电阻R2＝6Ω，虚线OO′下方是垂直于导轨平面的匀强磁场.现将质量m＝0.1kg、电阻不计的金属杆ab，从OO′上方某处垂直导轨由静止释放，杆下落0.2m过程中始终与导轨保持良好接触，加速度a与下落距离h的关系图象如图乙所示.求：

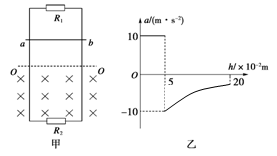
(1)磁感应强度B；
(2)杆下落0.2m过程中通过电阻R2的电荷量q.

参考答案：(1) 2T(2) 0.05C

本题解析：(1)由图象知，杆自由下落距离是0.05m，当地重力加速度g＝10m/s2，则杆进入磁场时的速度v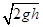＝＝1m/s
由图象知，杆进入磁场时加速度a＝－g＝－10m/s2
由牛顿第二定律得mg－F安＝ma
回路中的电动势E＝BLv
杆中的电流I＝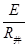 
R并＝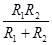
F安＝BIL＝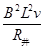 
得B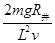＝＝2T
(2)杆在磁场中运动产生的平均感应电动势＝ 
杆中的平均电流＝ 
通过杆的电荷量Q＝·Δt 
通过R2的电量q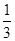＝Q＝0.05C
本题主要考查对电磁感应定律的应用，先根据图象得到杆进入磁场的速度，再根据牛顿定律求出磁场对杆的安培力，根据感应电动势和安培力的计算公式计算出磁感应强度，根据平均电流和时间计算出电荷量；

本题难度：困难