1、计算题  如图所示，长为31cm、内径均匀的细玻璃管开口向上竖直放置，管内水银柱的上端正好与管口齐平，封闭气体的长为10cm，温度为27℃，外界大气压强不变。若把玻璃管在竖直平面内缓慢转至开口竖直向下，这时留在管内的水银柱长为15cm，然后再缓慢转回到开口竖直向上，求：
（1）大气压强p0的值；　
（2）玻璃管重新回到开口竖直向上时空气柱的长度；　
（3）当管内气体温度升高到多少时，水银柱的上端恰好重新与管口齐平？

参考答案：解：（1）P1=P0+21cmHg，V1=10S，T1=300K，P2=P0－15cmHg，V2=10S，T2=300K
P1V1=P2V2
P0=75cmHg
（2）P3=75+15=90cmHg，V3=LS
P1V1=P3V3
L=10.67cm
（3）P4=P3=90cmHg，V4=（31－15）S=16S，T3=300K

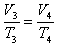
T4=450K，t=177℃

本题解析：

本题难度：一般

2、计算题  如图所示，A、B气缸的长度均为60 cm，截面积均为40 cm2，C是可在气缸内无摩擦滑动的、体积不计的活塞，D为阀门．整个装置均由导热材料制成．原来阀门关闭，A内有压强PA = 2.4×105 Pa的氧气．B内有压强PB = 1.2×105 Pa的氢气．阀门打开后，活塞C向右移动，最后达到平衡．（假定氧气和氢气均视为理想气体，连接气缸的管道体积可忽略，环境温度不变）求：

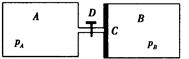
（1）活塞C移动的距离及平衡后B中气体的压强；   
（2）活塞C移动过程中B中气体是吸热还是放热（简要说明理由）．

参考答案：（1）20 cm   1.8×105 Pa （2）放热，理由见解析

本题解析：(1) 设活塞移动的距离为△L，平衡后B中气体压强为p。
由于平衡时，有，且装置导热，故为等温变化，根据玻意耳定律有：


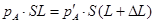
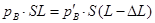
两式联立解得：△L=20 cm ；p=1.8×105 Pa
（2）气体放热，由于装置导热故T不变，而体积减小，活塞对B气体做功。根据热力学第一定律：
△U=Q+W
由于：△U=0；W>0
所以，Q<0，气体放热。
考点：本题考查气体的实验定律（玻意耳定律），热力学第一定律。

本题难度：一般

3、简答题  长为L的均匀玻璃管受重力为G。管的内壁是光滑的。管内有一个横截面积为S的轻活塞.在管中封闭有一定质量的气体.用细线把活塞吊起来，管竖直静止时,管内气柱长为,大气压强为.如果想把玻璃管和活塞分离,缓慢向下拉动玻璃管，在玻璃管上所加的竖直向下的的拉力至少为多大？

参考答案：

本题解析：
状态1如图甲，状态2如图乙。
以气体为研究对象 由玻马定律

以玻璃管为研究对象
状态1：
状态2：

本题难度：简单

4、计算题  （9分）如图所示，导热的圆柱形气缸放置在水平桌而上，横截面积为S、质量为ml的活塞封闭着一定质量的气体（可视为理想气体），活塞与气缸间无摩擦且不漏气。总质量为m2：的砝码盘（含砝码）通过左侧竖直的细绳与活塞相连。当环境温度为T时，活塞离缸底的高度为h。现使环境温度缓慢降为：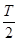

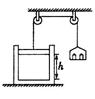
①当活塞再次平衡时，活塞离缸底的高度是多少?
②保持环境温度为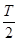不变，在砝码盘中添加质量为△m的砝码时，活塞返回到高度为h处，求大气压强p0。

参考答案：①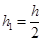②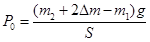

本题解析： ①环境温度缓慢降低过程中，气缸中气体压强不变，初始时温度为T1＝T，
体积为V1＝hS，变化后温度为，体积为V2＝h1S，由盖·吕萨克定律有
解得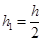
②设大气压强为p0，初始时体积V2＝h1S，压强
变化后体积V3＝hS，压强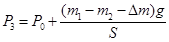
由玻意耳定律  p2V2＝p3V3
解得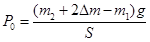
考点：盖·吕萨克定律；玻意耳定律

本题难度：一般

5、填空题  一定质量的气体，在体积不变的条件下，温度由0℃升高到10℃时，其压强的增量为△P1，当它由100℃升高到110℃时，所增加的压强为△P2，则△P1:△P2=___________。

参考答案：1：1

本题解析：

本题难度：简单