1、选择题 在光滑水平面上有两个的弹性小球A、B,质量都为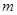 ,B球静止,A球向B球运动,发生正碰。已知碰撞过程中机械能守恒,两球压缩最紧时弹性势能为
,B球静止,A球向B球运动,发生正碰。已知碰撞过程中机械能守恒,两球压缩最紧时弹性势能为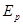 ,则碰前A速度等于 ( )
,则碰前A速度等于 ( )
A. 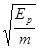 B.
B. 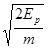 C.
C.  D.
D. 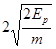
参考答案:C
本题解析:碰撞过程中动量守恒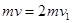 ,碰撞前后机械能守恒,当两个小球速度相同时,弹性势能最大,
,碰撞前后机械能守恒,当两个小球速度相同时,弹性势能最大, ,由两个公式联立的A的速度为
,由两个公式联立的A的速度为
本题难度:一般
2、简答题 静止的质量为M的原子核发生一次α衰变.已知衰变后的α粒子的质量为m、电荷量为q、速度为v,并假设衰变过程中释放的核能全部转化为α粒子和新核的动能.(注:涉及动量问题时,亏损的质量可忽略不计)
求:(1)衰变后新核反冲的速度大小;
(2)衰变过程中的质量亏损.
参考答案:(1)由动量守恒定律得:mv-(M-m)v"=0,
解得,新核的速度:v′=mM-mv;
(2)原子核衰变释放的能量:△E=12mv2+12(M-m)v′2,
由质能方程得:△E=△m?c2,
解得:△m=mMv22(M-m)c2;
答:(1)衰变后新核反冲的速度大小为mvM-m;
(2)衰变过程中的质量亏损为mMv22(M-m)c2.
本题解析:
本题难度:一般
3、计算题 (15分)如图所示的空间,匀强电场的方向竖直向下,场强为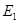 ,匀强磁场的方向水平向外,磁感应强度为
,匀强磁场的方向水平向外,磁感应强度为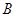 .有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为
.有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为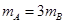 ,轨道半径为
,轨道半径为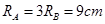 .
.
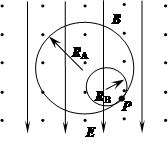
(1)试说明小球A和B带什么电,它们所带的电荷量之比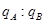 等于多少?
等于多少?
(2)指出小球A和B的绕行方向?
(3)设带电小球A和B在图示位置P处相碰撞,且碰撞后原先在小圆轨道上运动的带电小球B恰好能沿大圆轨道运动,求带电小球A碰撞后所做圆周运动的轨道半径(设碰撞时两个带电小球间电荷量不转移)。
参考答案:(1)两小球都带负电荷,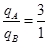 ?(2)两带电小球的绕行方向都相同?(3)
?(2)两带电小球的绕行方向都相同?(3)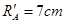
本题解析:
试题分析: (1)因为两带电小球都在复合场中做匀速圆周运动,故必有 ,由电场方向可知,两小球都带负电荷?(2分)
,由电场方向可知,两小球都带负电荷?(2分)
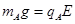
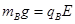 ?(1分)
?(1分)
且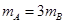
可得: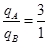 ?(2分)
?(2分)
(2)由题意可知,两带电小球的绕行方向都相同
由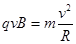 ?(2分)
?(2分)
得: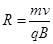
由题意有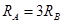 ?(1分)
?(1分)
解得: ?(2分)
?(2分)
(3)由于两带电小球在P处相碰,切向合外力为零,故两带电小球在相碰处的切向动量守恒,
有: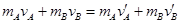 ?(2分)
?(2分)
解得: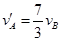 ?
?
而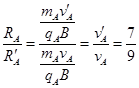 ?(1分)
?(1分)
所以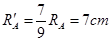 ?(2分)
?(2分)
本题难度:一般
4、计算题 (12分) 在光滑水平面上静置有质量均为m的木板AB和滑块CD,木板AB上表面粗糙,动摩擦因数为μ,滑块CD上表面为光滑的1/4圆弧,它们紧靠在一起,如图1-93所示.一可视为质点的物块P质量也为m,它从木板AB右端以初速v0滑入,过B点时速度为v0/2,后又滑上滑块,最终恰好滑到最高点C处,求:

(1)物块滑到B处时,木板的速度vAB;
(2)木板的长度L;
(3)物块滑到C处时滑块CD的动能.
参考答案:(1)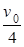 ;(2)
;(2)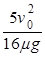 ;(3)
;(3)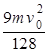
本题解析:(1)物体由A滑至B的过程中,由三者系统水平方向动量守恒得:
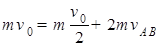 .解之得
.解之得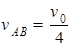 .
.
(2)物块由A滑至B的过程中,由三者功能关系得: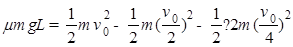 .
.
解之得 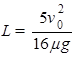 .
.
(3)物块由D滑到C的过程中,二者系统水平方向动量守恒,又因为物块到达最高点C时,物块与滑块速度相等且水平,均为v.
故得  ,
,
∴ 得滑块的动能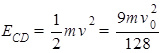 .
.
本题难度:一般
5、计算题 (8分)如图一砂袋用无弹性轻细绳悬于O点。开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出。第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ。若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求:两粒弹丸的水平速度之比V0/V为多少?
参考答案: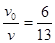
本题解析:弹丸击中砂袋瞬间,系统水平方向不受外力,动量守恒,设碰后弹丸和砂袋的共同速度为v1,细绳长为L,根据动量守恒定律有
mv0= (m+5m)v1?(2分)
砂袋摆动过程中只有重力做功,机械能守恒,所以
 ?(2分)
?(2分)
设第二粒弹丸击中砂袋后弹丸和砂袋的共同速度为v2
同理有:? mv-(m+5m)v1= (m+6m)v2 ?(1分)
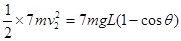 ?(1分)
?(1分)
联解上述方程得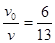 ?(2分)
?(2分)
本题考查动量守恒定律,在弹丸击中砂袋瞬间,弹丸与沙袋动量守恒,根据碰撞后黏在一体可求得末速度,之后整体获得向右的速度,向右摆动,摆动到最高点过程中整体机械能守恒,设最低点为零势面,找到初末状态列式求解
本题难度:一般