1、选择题  下列说法正确的是（　　）
A．做匀速圆周运动的物体，加速度大小保持不变，所以是匀变速（曲线）运动
B．匀速圆周运动的速度大小保持不变，所以匀速圆周运动的加速度为0
C．匀速圆周运动的加速度大小虽然不变，但方向始终指向圆心，加速度的方向发生了变化，所以匀速圆周运动既不是匀速运动，也不是匀变速运动
D．做匀速圆周运动的物体，虽然速度大小不变，但方向总是在改变，所以必有加速度

参考答案：A、匀速圆周运动加速度始终指向圆心，方向时刻在变化，加速度是变化的，所以匀速圆周运动是变加速运动，故AB错误；
C、匀速圆周运动速度大小不变，方向变化，速度是变化的，是变速运动，加速度也是变化的，所以匀速圆周运动既不是匀速运动，也不是匀变速运动，故CD正确．
故选：CD

本题解析：

本题难度：一般

2、选择题  如图所示，质量为m的小球置于正方体的光滑盒子中，盒子的边长略大于球的直径。某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，巳知重力加速度为g，空气阻力不计

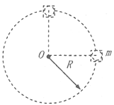
A．若盒子在最高点时，盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为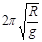
B．若盒子以速率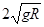做匀速圆周运动则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子左侧面的力为4mg
C．若盒子以角速度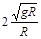做匀速圆周运动，则当盒子运动到最高点时，小球对盒子的下面的力为3mg
D．盒子从最低点向最髙点做匀速圆周运动的过程中，球处于超重状态；当盒子从最高点向最低点做匀速圆周运动的过程中，球处于失重状态

参考答案：A

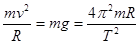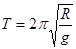本题解析：若盒子在最高点时，盒子与小球之间恰好无作用力，说明小球的重力提供向心力，，所以周期，所以A正确。若盒子以速率做匀速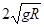圆周运动，运动到图示水平位置时，小球对盒子左侧无力的作用，对盒子右侧作用为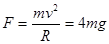。所以B错误。若盒子以角速度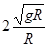做匀速圆周运动，当盒子运动到最高点时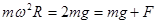，,所以小球对盒子上面的力为mg，所以C错误。盒子从最低点到最高点做匀速圆周运动分过程中，加速度一直改变，在水平位置前，超重，水平位置正常，之后失重，所以D错误。选A。

本题难度：简单

3、计算题  在沥青铺设的高速公路上，汽车的设计时速是108km/h。若汽车在这种路面上行驶时，轮胎与地面的最大静摩擦力等于车重的0.6.(取g＝10m/s2) 求：
（1）如果汽车在这种高速路上水平转弯，假设弯道的路面是水平的且拐弯时不产生横向滑动，则其弯道的最小半径应是多少？
（2）此高速路上有一圆弧形的拱形立交桥，要使汽车能够不离开地面安全通过圆弧拱桥，这个圆弧拱桥的半径应满足什么条件？

参考答案：(1) 150m(2) R≥90m.

本题解析：(1)汽车在水平路面上拐弯，可视为汽车做匀速圆周运动，其向心力是车与路面间的静摩擦力，（1分）
mv2/r≤0.6mg（1分）
由速度v＝30m/s，得弯道半径r≥150m；（1分）
故弯道的最小半径是150m(1分)
(2)汽车过拱桥，可视为在竖直平面内做匀速圆周运动，到达最高点时，
mv2/R＝mg－FN（1分）
为了保证安全，车对路面的压力FN必须大于等于零．（1分）
mv2/R≤mg，（1分）
则R≥90m.（1分）

本题难度：一般

4、选择题  关于匀速圆周运动的向心力，下列说法正确的是（   ）     
A 向心力是根据力的效果命名的
B 向心力可以是多个力的合力，也可以是其中的一个力或一个力的分力
C 对稳定的圆周运动，向心力是一个恒力      
D 向心力的效果是改变质点的线速度大小

参考答案：AB

本题解析：向心力时刻指向圆心，是变力，C错；向心力时刻与速度垂直，效果是改变质点的线速度的方向，D错；

本题难度：简单

5、计算题  如图所示，长l的细绳一端系质量m的小球，另一端固定于O点，细绳所能承受拉力的最大值是7mg．现将小球拉至水平并由静止释放，又知图中O′点有一小钉，为使小球可绕O′点做竖直面内的圆周运动．试求OO′的长度d与θ角应满足的关系(设绳与小钉O′相互作用中无能量损失)．

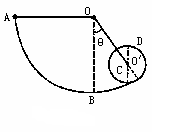
参考答案：

本题解析：本题考查圆周运动、动能定理、机械能守恒的应用，在临界状态的受力和特点是本题的难点，
设小球能绕O′点完成圆周运动，如图所示．其最高点为D，最低点为C．对于D点，依向心力公式有
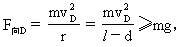? (1)（2分）
其中vD为D点速度，vD可由机械能守恒定律求知，取O点为重力势能的零势能位置，则
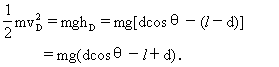（2）（2分）
将(1)式与(2)式联立，解之可得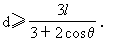（1分）
另依题意细绳上能承受的最大拉力不能超过7mg，由于在最低点C，绳所受拉力最大，故应以C点为研究对象，并有
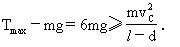（3）?（1分）?其中vC是C点速度，
可由机械能守恒定律求知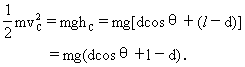(4) （2分）
将(3)式与(4)式联立，解之可得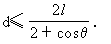（1分）
（1分）

本题难度：一般