1、选择题  做匀速圆周运动的物体，下列不变的物理量是
[? ]
A．速度
B．速率
C．角速度
D．周期

参考答案：BCD

本题解析：

本题难度：简单

2、选择题  如图所示，放在水平转盘上的物块随转盘一起匀速转动，物块的向心力是

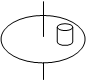
A．重力
B．静摩擦力
C．重力和支持力的合力
D．离心力

参考答案：B

本题解析：物体在水平转盘上随转盘一起匀速转动，竖直方向上重力和支持力保持平衡，水平方向上受到转盘给的向里的静摩擦力，所以物体的向心力是静摩擦力提供的。

本题难度：简单

3、填空题  如图所示皮带转动轮，大轮直径是小轮直径的2?倍，A是大轮边缘上一点，B是小轮边缘上一点，C是大轮上一点C到圆心O1的距离等于小轮半径。转动时皮带不打滑，则A、B、C三点的角速度之比ωA：ωB： ωC=__? __? ___，向心
加速度大小之比aA：aB：aC=____??。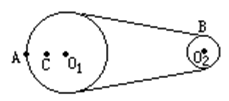

参考答案：2：4：1?1：2：1

本题解析：分析：靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度．根据v=rω，a=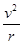和a=rω2可得出A、B、C三点的角速度之比和向心加速度之比．
解答：解：A、B两点的线速度相等，A的半径是B的半径的2倍，根据v=rω，知ωA：ωB=1：2．A、C共轴转动，角速度相等，即ωA：ωC=1：1．所以ωA：ωB：ωC=1：2：1．
A、B两点的线速度相等，A的半径是B的半径的2倍，根据a=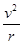，知aA：aB=1：2，A、C具有相同的角速度，根据a=rω2，知aA：aC=2：1．所以aA：aB：aC=2：4：1．
故答案为：1：2：1，2：4：1．
点评：解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度．掌握线速度与角速度的关系，以及线速度、角速度与向心加速度的关系．

本题难度：一般

4、选择题  放置在同一竖直面内的两光滑同心圆环a、b通过过其圆心的竖直轴O1O2连接，其半径Rb=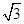Ra，环上各有一个穿孔小球A、B(图中B球未画出)，均能沿环无摩擦滑动。如果同心圆环绕竖直轴O1O2以角速度ω匀速旋转，两球相对于铁环静止时，球A所在半径OA与O1O2成θ=300角。则(   )

A.球B所在半径OB与O1O2成45°角
B.球B所在半径OB与O1O2成30°角
C.球B和球A在同一水平线上
D.由于球A和球B的质量未知，不能确定球B的位置

参考答案：C

本题解析：
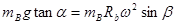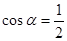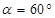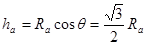a小球的受力分析如图所示 ，则，同理b物体有 ，解得， ，而 ，而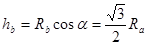 ，故球B和球A在同一水平线上，选项C正确。
考点：匀速圆周运动

本题难度：一般

5、计算题  如图所示，一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线的夹角θ＝30°，一条长为l的绳，一端固定在圆锥体的顶点O，另一端系一个质量为m的小球(视作质点)，小球以速率v绕圆锥体的轴线做水平匀速圆周运动，则

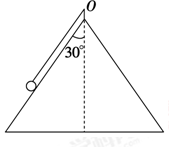
(1)当v1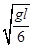＝时，绳对小球的拉力多大？
(2)当v2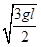＝时，绳对小球的拉力多大？

参考答案：（1）1.03mg；（2）2mg；

本题解析：如图(甲)所示，小球在锥面上运动，锥面对小球恰好无压力时，重力mg和绳的拉力FT提供向心力，根据牛顿第二定律得mgtan30°＝
解得v0＝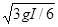

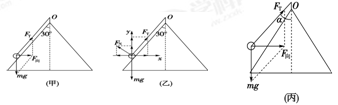
(1)因v1<v0，所以此时小球与锥面接触并产生弹力FN，受力情况如图(乙)所示，则
FTsin30°－FNcos30°＝
FTcos30°＋FNsin30°＝mg
联立解得FT＝1.03mg。
(2)因v2>v0，所以此时小球与锥面脱离，设绳与轴线的夹角为α，小球受力如图(丙)所示，则
FTsinα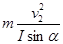＝        FTcosα＝mg     联立解得FT＝2mg
考点：向心力、牛顿第二定律

本题难度：一般