1、简答题  在间距d=0.1m、电势差U=103V的两块竖立平行板中间，用一根长L=0.01m的绝缘细线悬挂一个质量m=0.2g、电量q=10-7C的带正电荷的小球，将小球拉到使丝线恰呈水平的位置A后由静止释放（如图所示），问：
（1）小球摆至最低点B时的速度和线中的拉力多大？
（2）若小球摆至B点时丝线突然断裂，以后小球能经过B点正下方的C点（C点在电场内，小球不会与正电荷极板相碰，不计空气阻力），则BC相距多远？（g=10m/s2）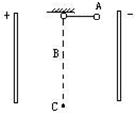

参考答案：（1）小球由静止释放后到摆到最低点的过程，由动能定理得
? ?mgL-EqL=12mv2?
? 又E=Ud，
? 代入解得v=

本题解析：

本题难度：一般

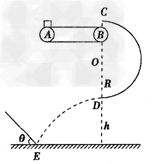
2、计算题  如图所示，一质量为m＝1 kg的小物块轻轻放在水平匀速运动的传送带上的A点，随传送带运动到B点，小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动．已知圆弧半径R＝0.9m，轨道最低点为D，D点距水平面的高度h＝0.8m．小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板．已知物块与传送带间的动摩擦因数μ＝0.3，传送带以5 m／s恒定速率顺时针转动（g取10 m／s2），试求：
（1）传送带AB两端的距离；
（2）小物块经过D点时对轨道的压力的大小；
（3）倾斜挡板与水平面间的夹角θ的正切值．

参考答案：解：（1）对小物块，在C点恰能做圆周运动，由牛顿第二定律得：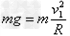
则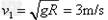
由于，小物块在传送带上一直加速，则由A到B有
，
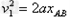
所以传送带AB两端的距离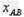=1.5m
（2）对小物块，由C到D有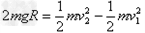
在D点FN-mg=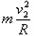，代入数据解得FN＝60N
由牛顿第三定律知小物块对轨道的压力大小为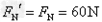
（3）小物块从D点抛出后做平抛运动，则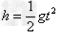，解得t＝0.4s
将小物块在E点的速度进行分解得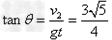

本题解析：

本题难度：一般

3、选择题  如图所示，质量为m2的物体，放在沿平直轨道向左行驶的车厢底板上，并用竖直细绳通过光滑的定滑轮连接质量为m1的物体。当车向左加速运动时，与物体m1相连接的绳与竖直方向成θ角，m2与车厢相对静止。则: (? )

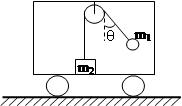
A．车厢的加速度为gsinθ
B．绳对物体m1的拉力为m1g/cosθ
C．底板对物体m2的支持力为（m2-m1）g
D．物体m2所受底板的摩擦力为m2gtanθ

参考答案：BD

本题解析：车厢水平向左做加速直线运动，两物体与车厢具有相同的加速度，由隔离法对分析，得出的加速度以及细线的拉力，从而得知车厢的加速度．再隔离对分析，求出支持力和摩擦力的大小。
AB、由于与车厢具有相同的加速度，对受力分析，受重力和拉力，根据合成法知，，拉力．的加速度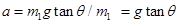，所以车厢的加速度为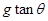；B正确
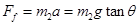CD、由于与车厢具有相同的加速度，对受力分析，受重力、拉力、支持力和摩擦力，则支持力为：,摩擦力为：；D正确
故选BD
点评：注意两物体与车厢有相同的加速度，通过整体法和隔离法进行求解。

本题难度：一般

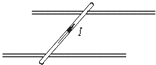
4、简答题  质量为1kg的金属杆静止于相距1m的两水平轨道上，金属杆中通有方向如图所示．大小为20A的恒定电流，两轨道处于竖直方向的匀强磁场中．金属杆与轨道间的动摩擦因数为0.6．（g取10m/s2）
（1）欲使杆向右匀速运动，求磁场的磁感应强度大小和方向
（2）欲使杆向右以加速度为2m/s2作匀加速运动，求磁场的磁感应强度大小．

参考答案：（1）杆向右匀速运动，说明杆受到的安培力是向右的，根据左手定则可以知道，磁场的方向竖直向上，大小和杆受到的摩擦力大小相等，
所以BIL=μmg，
所以B=μmgIL=0.6×1×1020×1T=0.3T．
（2）欲使杆向右以加速度为2m/s2作匀加速运动，由牛顿第二定律可知
B′IL-μmg=ma
B′=ma+μmgIL=1×2+0.6×1×1020×1T=0.4T
答：（1）欲使杆向右匀速运动，求磁场的磁感应强度大小为0.3T和方向竖直向上．
（2）欲使杆向右以加速度为2m/s2作匀加速运动，求磁场的磁感应强度大小为0.4T．

本题解析：

本题难度：一般

5、填空题  用3N的水平拉力拉一个物体沿水平地面运动时，物体的加速度为1m/s2，改用4N的水平拉力拉时，它的加速度为2m/s2，那么改用5N的水平拉力拉它时，加速度将是______m/s2，物体与地面的动摩擦因数是______．

参考答案：根据牛顿第二定律得，F1-f=ma1，即3-f=m，
F2-f=ma2，即4-f=2m
联立两式解得f=2N，m=1kg．
动摩擦因数μ=fmg=0.2．
根据牛顿第二定律得，a3=F3-fm=5-21=3m/s2．
故答案为：3，0.2．

本题解析：

本题难度：一般