1、选择题 如果人造卫星进入地面附近的轨道速度大于7.9km/s,而小于?11.2km/s,它绕地球运动是( )
A.圆
B.椭圆
C.双曲线中一支
D.抛物线
参考答案:B
本题解析:
本题难度:一般
2、简答题 某人在一星球上以速度υ0竖直上抛一物体,设t秒钟后物体落回手里,已知星球的半径为R,那么至少要用多大的速度沿星球表面抛出,才能使物体不再落回星球表面?
参考答案:小球做竖直上抛运动,则
由v0=g?t2
解得:g=2v0t
星球表面的小球所受重力等于星球对小球的吸引力,
则由mg=GMmR2
得M=gR2G
现将此球沿此星球表面将小球水平抛出,欲使其不落回星球,则抛出时的速度至少为该星球的第一宇宙速度,
物体在星球表面附近能做匀速圆周运动,其向心力由星球的吸引力提供,
则由GMmR2=mv2R
v=
本题解析:
本题难度:一般
3、填空题 某星球的质量是地球的2倍,其半径是地球的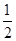 。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。
。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。
参考答案:2?;? 8
本题解析:第一宇宙速度就是环绕星球表面作圆周运动的速度,根据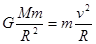 ,解得
,解得 ;所以
;所以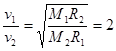 ;根据
;根据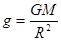 ,所以
,所以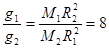 。
。
本题难度:简单
4、简答题 人造地球卫星绕地球旋转(设为匀速圆周运动)时,既具有动能又具有引力势能(引力势能实际上是卫星与地球共有的,简略地说此势能是人造卫星所具有的)。设地球的质量为M,以卫星离地还需无限远处时的引力势能为零,则质量为m的人造卫星在距离地心为r处时的引力势能为 (G为万有引力常量)。
(G为万有引力常量)。
(1)试证明:在大气层外任一轨道上绕地球做匀速圆周运动的人造卫星所具有的机械能的绝对值恰好等于其动能。
(2)当物体在地球表面的速度等于或大于某一速度时,物体就可以挣脱地球引力的束缚,成为绕太阳运动的人造行星,这个速度叫做第二宇宙速度,用v2表示。用R表示地球的半径,M表示地球的质量,G表示万有引力常量.试写出第二宇宙速度的表达式。
(3)设第一宇宙速度为v1,证明: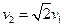 。
。
参考答案:(1)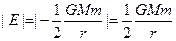 ?(2)
?(2)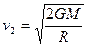
(3)第一宇宙速度即为绕地球表面运行的速度,故有:
 ?
?
得 ?所以有:
?所以有: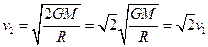
本题解析:(1)设卫星在半径为r的轨道上做匀速圆周运动的速度为v,地球的质量为M,
卫星的质量为m。有万有引力提供卫星做圆周运动的向心力:
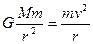 ?
?
所以,人造卫星的动能: ? ?
? ?
卫星在轨道上具有的引力势能为: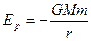 ?
?
所以卫星具有的机械能为:
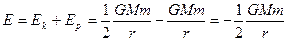 ?
?
所以: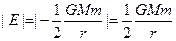 ?
?
(2)设物体在地于表面的速度为v2,当它脱离地球引力时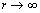 ,此时速度为零,由机械能守恒定律得:
,此时速度为零,由机械能守恒定律得:
 ?
?
得: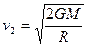 ?
?
(3)第一宇宙速度即为绕地球表面运行的速度,故有:
 ?
?
得 ?所以有:
?所以有: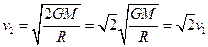
本题难度:一般
5、选择题 月球的质量约为地球的1/81,半径约为地球半径的1/4,地球上第一宇宙速度约为7.9km/s,则月球上第一宇宙速度约为多少?
参考答案: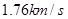
本题解析:根据万有引力提供向心力即 ,
,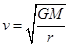
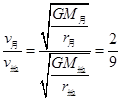
所以月球上第一宇宙速度为是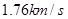
点评:本题关键是根据第一宇宙速度和重力加速度的表达式列式求解,
本题难度:简单