1、简答题  如图20所示，绝缘长方体B置于水平面上，两端固定一对平行带电极板，极板间形成匀强电场E。长方体B的上表面光滑，下表面与水平面的动摩擦因数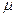=0.05（设最大静摩擦力与滑动摩擦力相同）。B与极板的总质量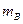=1.0kg.带正电的小滑块A质量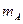=0.60kg，其受到的电场力大小F=1.2N.假设A所带的电量不影响极板间的电场分布。t=0时刻，小滑块A从B表面上的a点以相对地面的速度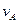=1.6m/s向左运动，同时，B（连同极板）以相对地面的速度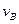=0.40m/s向右运动。问（g取10m/s2）
（1）A和B刚开始运动时的加速度大小分别为多少？
（2）若A最远能到达b点，a、b的距离L应为多少？从t=0时刻至A运动到b点时，摩擦力对B做的功为多少？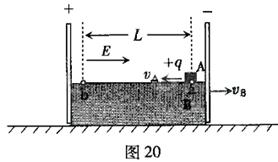

参考答案：见解析

本题解析：⑴由牛顿第二定律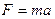有
A刚开始运动时的加速度大小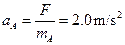?方向水平向右
B刚开始运动时受电场力和摩擦力作用
由牛顿第三定律得电场力
摩擦力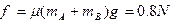
B刚开始运动时的加速度大小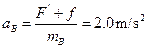方向水平向左
⑵设B从开始匀减速到零的时间为t1，则有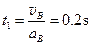
此时间内B运动的位移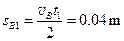
t1时刻A的速度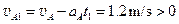，故此过程A一直匀减速运动。
此t1时间内A运动的位移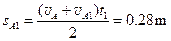
此t1时间内A相对B运动的位移
此t1时间内摩擦力对B做的功为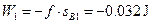
t1后，由于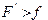，B开始向右作匀加速运动，A继续作匀减速运动，当它们速度相等时A、B相距最远，设此过程运动时间为t2，它们速度为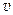，则有
对A?速度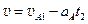www.
对B?加速度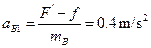
速度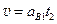
联立以上各式并代入数据解得?
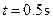
此t2时间内A运动的位移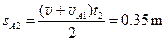
此t2时间内B运动的位移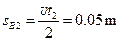
此t2时间内A相对B运动的位移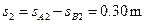
此t2时间内摩擦力对B做的功为
所以A最远能到达b点a、b的距离L为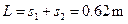
从t=0时www.刻到A运动到b点时，摩擦力对B做的功为
。

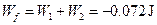本题难度：简单

2、计算题  .如图所示是示波器的部分构造示意图，真空室中阴极K不断发出初速度可忽略的电子，电子经电压U0=1.82×l04V的电场加速后，由孔N沿长L=0.10m相距为d="0.020" m的两平行金属板A、B间的中心轴线进入两板间，电了穿过A、B板后最终可打在中心为O的荧光屏CD上，光屏CD距A、B板右侧距离s=0.45m.若在A、B间加UAB=54.6V的电压.已知电子电荷最e=1.6×10-19C，质量m=9.1×10-31kg。求：

（1）电子通过孔N时的速度大小；
（2）荧光屏CD上的发光点距中心O的距离。

参考答案：（1）；（2）

本题解析：（1）设电子通过加速电场到达N孔的速度大小为v，根据动能定理得: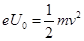
解得：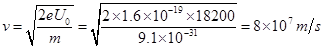 
（2）设电子通过加速电场的最大偏移为y，由类平抛规律得: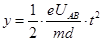

解得： 
设荧光屏上发光点到O点的距离为Y，打在荧光屏上的电子相当于从A、B板中心沿直线射出.由几何关系得：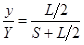
解得：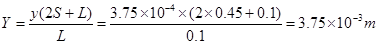 
考点：带电粒子在电场中的加速和偏转.

本题难度：一般

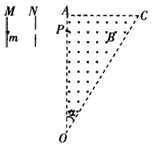
3、计算题  如图所示，直角三角形OAC（α=30°）区域内有B=0.5 T的匀强磁场，方向如图所示，两平行极板M，N接在电压为U的直流电源上，左板为高电势，一带正电的粒子从靠近M板由静止开始加速，从N板的小孔射出电场后，垂直OA的方向从P点进入磁场中。带电粒子的比荷为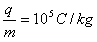，OP间距离为L=0.3 m，全过程不计粒子所受的重力，则：
(1)若加速电压U=120 V，通过计算说明粒子从三角形OAC的哪一边离开磁场？
(2)求粒子分别从OA，OC边离开磁场时粒子在磁场中运动的时间。

参考答案：解：(1)如图所示，当带电粒子的轨迹与OC边相切时为临界状态，设临界关径为R，加速电压U0，则有

，解得R=0.1 m


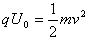
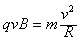
U0=125 V
U＜U0，则r＜R，粒子从OA边射出
(2)带电粒子在磁场做圆周运动的周期为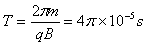
当粒子从OA边射出时，粒子在磁场中恰好运动了半个周期
当粒子从OC边射出时，粒子在磁场中运动的时间小于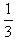周期

本题解析：

本题难度：困难

4、计算题  （10分）电视机中显像管（抽成真空玻璃管）的成像原理主要是靠电子枪产生高速电子束，并在变化的磁场作用下发生偏转，打在荧光屏不同位置上发出荧光而形成像。显像管的原理示意图（俯视图）如图甲所示，在电子枪右侧的偏转线圈可以产生使电子束沿纸面发生偏转的磁场，偏转的磁场可简化为由通电螺线管产生的与纸面垂直的磁场，该磁场分布的区域为圆形（如图乙所示），其磁感应强度B=μNI，式中μ为磁常量，N为螺线管线圈的匝数，I为线圈中电流的大小。由于电子的速度极大，同一电子穿过磁场过程中可认为磁场没有变化，是稳定的匀强磁场。

已知电子质量为m，电荷量为e，电子枪加速电压为U，磁常量为μ，螺线管线圈的匝数N，偏转磁场区域的半径为r，其圆心为O点。当没有磁场时，电子束通过O点，打在荧光屏正中的M点，O点到荧光屏中心的距离OM=L。若电子被加速前的初速度和所受的重力、电子间的相互作用力以及地磁场对电子束的影响均可忽略不计，不考虑相对论效应及磁场变化所激发的电场对电子束的作用。
（1）求电子束经偏转磁场后打到荧光屏上P点时的速率；
（2）若电子束经偏转磁场后速度的偏转角θ=60°，求此种情况下电子穿过磁场时，螺线管线圈中电流I0的大小；
（3）当线圈中通入如图丙所示的电流，其最大值为第（2）问中电流的0.5倍。求电子束打在荧光屏上发光所形成“亮线”的长度。

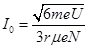参考答案：（1） （2） （3）

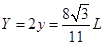
本题解析：（1）设经过电子枪加速电场加速后，电子的速度大小为v。
根据动能定理有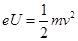： （2分）
解得：    （1分）
（2）设电子在磁场中做圆运动的半径为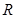，运动轨迹如图所示。

根据几何关系有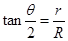：（1分）
洛伦兹力提供向心力，根据牛顿第二定律有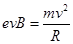：（1分）
由题知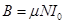
解得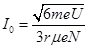： （1分）
（3）设线圈中电流为0.5I0时，偏转角为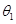，此时电子在屏幕上落点距M点最远。
此时磁感应强度，
轨迹圆半径（1分）
 （1分）
电子在屏幕上落点距M点最远距离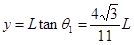（1分）
亮线长度 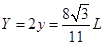（1分）
考点：本题考查带电粒子在复合场中的运动

本题难度：困难

5、选择题  有一种飞行器是利用电场加速带电粒子，形成向外发射的高速粒子流，对飞行器自身产生反冲力，从而对飞行器的飞行状态进行调整的。已知飞行器发射的高速粒子流是由二价氧离子构成的。当单位时间内发射的离子个数为n，加速电压为U时，飞行器获得的反冲力为F。为了使加速器获得的反冲力变为2F，只需要
[? ]
A．将加速电压变为2U
B．将加速电压变为4U
C．将单位时间内发射的离子个数变为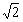n
D．将单位时间内发射的离子个数变为4n

参考答案：B

本题解析：

本题难度：一般