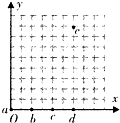
1、填空题  如图所示，边长为L的正方形区域abcd内存在着匀强磁场．
一个质量为m、电荷量为q、初速度为vo的带电粒子从a点沿ab方向进入磁场，不计重力．若粒子恰好沿BC方向，从c点离开磁场，则磁感应强度B=______；粒子离开磁场时的动能为Ex=______．

参考答案：由几何关系得，粒子在磁场中运动的半径r=L．
根据qvB=mv02L
解得B=mv0qL．
带电粒子在磁场中运动的速度大小不变，所以动能EK=12mv02．
故答案为：mv0qL，mv022．

本题解析：

本题难度：简单

2、简答题  如图所示，虚线为有界磁场的竖直界面所在处，其区域宽度为d，磁场磁感应强度为B方向垂直纸面向里．有一带电粒子从磁场中央O点出发，粒子速度大小为v，方同垂直磁场且与水平方向成30°角粒子质量为m电荷量为q，不计粒子重力若要求粒子能从左边边界射出磁场，则对粒子速度v的要求如何？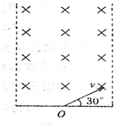

参考答案：带电粒子在匀强磁场中由洛伦兹力提供向心力，做匀速圆周运动，则有? qvB=mv2R，得粒子的轨迹为 R=mvqB


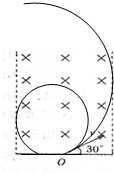
（1）若粒子做圆周运动恰好经过左边边界并且瞬时速度与边界线相切，则其对应轨迹如右图所示，设粒子对应速度大小为v1，轨道半径为R1，根据粒子对应速度大小为v1，轨道半径为R1，根据粒子经过O、A两点的速度方向确定圆弧轨迹圆心O1，由数学关系有
? R1+R1cos60°=d2
得? R1=d3
由R1=mv1qB得，v1=qBd3m
要使粒子从左边界射出磁场，其运动轨迹的半径应大于R1，因此粒子运动速度 v＞qBd3m．
（2）若粒子做圆周运动经过右边边界并且速度方向恰好与边界相切，则其运动轨迹如右图所示，设其对应的速度大小为v2，轨道半径为R2．利用作图法确定轨迹圆心O2，则数学关系有：R2cos60°+d2=R2
得? R2=d
由R2=mv2qB得? v2=qBdm
要使粒子从不从右边边界射出，其运动轨道半径应小于R2，因此对速度大小要求v＜qBdm．
综上所述，对粒子运动速度大小取值要求为?qBd3m＜v＜qBdm．
答：粒子速度v的范围为 qBd3m＜v＜qBdm．

本题解析：

本题难度：一般

3、选择题  飞机在水平地面上空的某一高度水平匀速飞行，每隔相等时间投放一个物体．如果以第一个物体a的落地点为坐标原点、飞机飞行方向为横坐标的正方向，在竖直平面内建立直角坐标系．如图所示是第5个物体e离开飞机时，抛出的5个物体（a、b、c、d、e）在空间位置的示意图，其中可能的是（　　）
A．

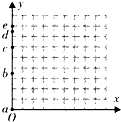
B．

C．

D．

参考答案：不计空气阻力，以地面为参考系，每个物体都做平抛运动，水平方向做匀速直线运动，所以在水平方向上，四个物体的速度总是与飞机速度相同的，水平位移相同，故没有位移差，看起来在一条竖直线上；竖直方向做自由落体运动，最先释放的物体间的距离大些，相当于同一个物体做自由落体运动在不同时刻的位置，故A正确，B错误，
若第5个物体e离开飞机时，c刚好落地，此时对于C图，若第5个物体e离开飞机时，d刚好落地，此时对于D图，故CD正确
故选ACD．

本题解析：

本题难度：简单

4、选择题  长l的细绳一端固定，另一端系一个小球，使球在竖直平面内做圆周运动，那么（　　）
A．小球通过圆周上顶点时的速度最小可以等于零
B．小球通过圆周上顶点时的速度最小不能小于

参考答案：A、在最高点，临界情况是绳子的拉力为零，有：mg=mv2l．解得v=

本题解析：

本题难度：一般

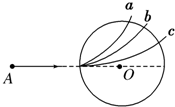
5、选择题  圆形区域内有垂直于纸面的匀强磁场，三个质量和电荷量都相同的带电粒子a、b、c，以不同的速率沿着AO方向对准圆心O射入磁场，其运动轨迹如图所示．若带电粒子只受磁场力的作用，则下列说法正确的是（　　）
A．a粒子速率最大
B．c粒子速率最小
C．a粒子在磁场中运动的时间最长
D．它们做圆周运动的周期Ta＜Tb＜Tc