1、简答题  如图所示，AB为水平轨道，A、B间距离s=1.25m，BCD是半径为R=0.40m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．有一小物块质量为m=1.0kg，小物块在F=10N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，它与水平轨道和半圆形轨道间的摩擦均不计．g取10m/s2，求：
（1）撤去力F时小物块的速度大小；
（2）小物块通过D点瞬间对轨道的压力大小；
（3）小物块通过D点后，再一次落回到水平轨道AB上，落点和B点之间的距离大小．

参考答案：（1）当物块从A滑向B时，设在B点撤去F时速度大小为vB．
根据动能定理得：Fs=12mv2B
得 vB=5m/s
（2）小物块从B到D点瞬间，由动能定理得：
-mg?2R=12mv2D-12mv2B
解得：vD=3m/s
根据牛顿第二定律得：
? FD+mg=mv2DR
解得：FD=12.5N?
由牛顿第三定律知压力大小为FD′=FD=12.5N
（3）物块通过D点后做平抛运动，有：
?2R=12gt2
?x=vDt
解得：x=1.2m
答：（1）撤去力F时小物块的速度大小是5m/s；
（2）小物块通过D点瞬间对轨道的压力大小是12.5N；
（3）小物块通过D点后，再一次落回到水平轨道AB上，落点和B点之间的距离大小是1.2m．

本题解析：

本题难度：一般

2、填空题  质量相等的A ，B 两质点分别做匀速圆周运动，若在相等的时间内通过的弧长之比为2:3 ，而转过的角度之比为3 ：2 ，则A ，B 两质点周期之比TA ：TB=__? _ ，向心加速度之比aA ：aB=__? __ 。

参考答案：2 : 3；1: 1

本题解析：

本题难度：一般

3、简答题  科学家在地球轨道外侧发现了一颗绕太阳运行的小行星，经过观测该小行星每隔t时间与地球相遇一次（即距离最近），已知地球绕太阳公转半径是R，周期是T，设地球和小行星都是圆轨道，且在同一个面同向转动，求
（1）太阳的质量
（2）小行星与地球的最近距离．

参考答案：地球绕太阳运动GMmR2=m4π2RT2?
故太阳的质量为：M=4π2R3GT2?
（2）设小行星运行周期为T1，tT-tT1=1
对小行星，有：GMm1R12=m14π2R1T12?
解得：R1=3t2(t-T)2R

本题解析：

本题难度：一般

4、简答题  如图所示，小球在竖直放置的光滑圆形管道内做圆周运动，管道内侧壁半径为R，小球半径为r，当小球以初速度V0从管道最低点出发，到最高点时恰好对管道无压力，求：V0的大小．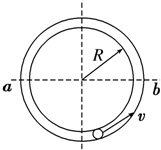

参考答案：小球在最高点恰好无压力，则mg=mv2R+r?①
从最低点到最高点的过程中，只有重力做功，由机械能守恒得：
12mv02=mg2（R+r）+12mv2?②
由①、②两式解得
V0=

本题解析：

本题难度：一般

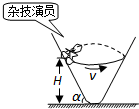
5、选择题  “飞车走壁”杂技表演比较受青少年的喜爱，这项运动由杂技演员驾驶摩托车，简化后的模型如图所示，表演者沿表演台的侧壁做匀速圆周运动．若表演时杂技演员和摩托车的总质量不变，摩托车与侧壁间沿侧壁倾斜方向的摩擦力恰好为零，轨道平面离地面的高度为H，侧壁倾斜角度α不变，则下列说法中正确的是（　　）
A．摩托车做圆周运动的H越高，向心力越大
B．摩托车做圆周运动的H越高，线速度越大
C．摩托车做圆周运动的H越高，向心力做功越多．
D．摩托车对侧壁的压力随高度H变大而减小