1、计算题 (2011年昆明模拟)如图甲所示,在倾角为30°的足够长光滑斜面AB前,有一粗糙水平面OA,OA长为4 m.有一质量为m的滑块,从O处由静止开始受一水平向右的力F作用.F按图乙所示的规律变化.滑块与OA间的动摩擦因数μ=0.25,g取10 m/s2,试求:

(1)滑块到A处的速度大小;
(2)不计滑块在A处的速率变化,滑块冲上斜面AB的长度是多少?
参考答案:(1)5  ?m/s (2)5 m
?m/s (2)5 m
本题解析:(1)由题图乙知,在前2 m内,F1=2mg,做正功;
在第3 m内,F2=-0.5mg,做负功;
在第4 m内,F3=0.
滑动摩擦力
Ff=-μmg=-0.25mg,始终做负功.
对OA过程由动能定理列式得
F1x1+F2x2+Ff·x=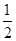 ?mv-0.
?mv-0.
即2mg×2-0.5mg×1-0.25mg×4=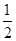 ?mv,
?mv,
解得vA=5  ?m/s.
?m/s.
(2)冲上斜面的过程,由动能定理得
-mg·L·sin30°=0-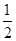 ?mv,
?mv,
所以冲上斜面AB的长度L=5 m.
本题难度:一般
2、简答题 如图所示是某公园中的一项游乐设施,半径为R=手.5m、r=4.5m的两圆形轨道甲和乙安装在同一竖直平面内,两轨道之间由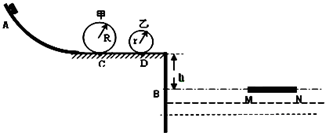 一条水平轨道CD相连,现让可视为质点的质量为40图g的无动力小滑车从A点由静止释放,刚好可以滑过甲轨道后经过CD段又滑手乙轨道后离开两圆形轨道,然后从水平轨道飞入水池内,水面离水平轨道的高度h=5m,所有轨道均光滑,g=40m/s手.
一条水平轨道CD相连,现让可视为质点的质量为40图g的无动力小滑车从A点由静止释放,刚好可以滑过甲轨道后经过CD段又滑手乙轨道后离开两圆形轨道,然后从水平轨道飞入水池内,水面离水平轨道的高度h=5m,所有轨道均光滑,g=40m/s手.
(4)求小球到甲轨道最高点时的速度v.
(手)求小球到乙轨道最高点时对乙轨道的压力.
(3)若在水池中MN范围放手安全气垫(气垫厚度不计),水面手的4点在水平轨道边缘正下方,且4M=40m,4N=45m;要使小滑车能通过圆形轨道并安全到达气垫手,则小滑车起始点A距水平轨道的高度该如何设计?
参考答案:(1)在C轨道最高点:1g=1v2R
解得:v=51/s
即6车通过C轨道最高点的速度为51/s;
(2)从C轨道最高点到D轨道最高点过程,根据动能定理,有:
1g(2R-2r)=121v2D-121v2
在D轨道最高点:
1g-N=1v2Dr
解得:N=333.3N
由牛顿第三定律知,6车对轨道的压力为333.3N;
(3)6滑车要安全通过圆形轨道,在平台上的速度至b为v0,从释放到平抛初位置过程,根据动能定理,有:
1g左=121v20 ①
从开始释放到C轨道最高点过程,根据动能定理,有
1g(左-2R)=121v2C′②
要能通过圆轨道,有
vC′>51/s ③
对于平抛运动,有:
左=12gt2 ④
S=v0t ⑤
由①②③④⑤解得
左=d.21
答:(1)6球到甲轨道最高点时的速度为51/s.
(2)6球到乙轨道最高点时对乙轨道的压力为333.3N.
(3)6滑车至b应从离水平轨道d.21的中方开始下滑.
本题解析:
本题难度:简单
3、简答题 如图所示,倾角为θ的光滑斜面上有轻杆连接的A、B两个小物体,A的质量为m,B的质量为3m,轻杆长为L,A物体距水平地面的高度为h,水平地面光滑,斜面与水平地面的连接处是光滑圆弧,两物体从静止开始下滑.求:
(1)两物体在水平地面上运动时的速度大小?
(2)在整个运动过程中,杆对B物体所做的功?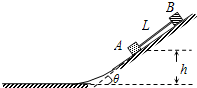
参考答案:(1)A、B一起从斜面运动到水平地面的过程中,机械能守恒,设在水平地面上的共同速度为v,则
mgh+3mg(h+Lsinθ)=12(m+3m)v2
解得v=
本题解析:
本题难度:一般
4、计算题 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的第一象限,存在以x轴y轴及双曲线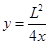 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场I;在第二象限存在以x=-L; x=-2L;y=0;y=L的匀强电场II.两个电场大小均为E,不计电子所受重力.求
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场I;在第二象限存在以x=-L; x=-2L;y=0;y=L的匀强电场II.两个电场大小均为E,不计电子所受重力.求
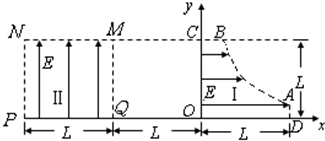
(1)从电场I的边界B点处由静止释放电子,电子离开MNPQ时的位置;
(2)由电场I的AB曲线边界处由静止释放电子离开MNPQ时的最小动能;
参考答案:(1)电子从P点射出?(2)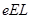
本题解析:(1)据题意,B点纵坐标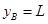 ,根据双曲线方程
,根据双曲线方程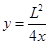 得到,横坐标
得到,横坐标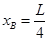 ,
,
电子从B运动到C过程,根据动能定理得: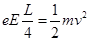 ,
,
电子在MNPQ区域做类平抛运动,水平方向: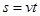 ,竖直方向:
,竖直方向: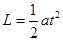 ,
,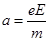
解得: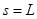 ,即电子从P点射出。
,即电子从P点射出。
(2)设释放位置坐标为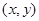 ,则有:
,则有: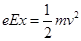 ,
,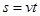 ,
,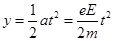 ,解得:
,解得: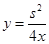
又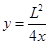 ,得到:
,得到: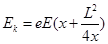 ,
,
根据数学知识得知,当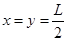 时,动能
时,动能 有最小值
有最小值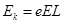 。
。
本题难度:一般
5、计算题 两平行板间有水平匀强电场,一根长为L=0.1m,不可伸长的不导电细绳的一端连着一个质量为 m=0.1g、带电量为q=5x10-6C的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ=37°求

(1) 匀强电场的场强大小
(2)经过最低点时,小球对细线的拉力.
参考答案:(1)100N/C(2)2x10-3N,方向沿绳子向上
本题解析:(1)小球从水平摆到最左侧过程中,由动能定理有:
 ?①(2分)
?①(2分)
 ?="100N/C" ?(1分)
?="100N/C" ?(1分)
(2)小球从水平摆到最左侧过程中,由动能定理有:
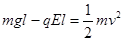 ?②(2分)
?②(2分)
在最低点由向心力公式有: ?③(2分)
?③(2分)
由①②③得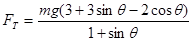 =2x10-3N(1分)
=2x10-3N(1分)
由牛顿第三定律有:小球对细线的拉力大小为2x10-3N,方向沿绳子向上。(2分)
点评:小球从静止释放后沿圆弧运动到最低点,说明小球一定带正电.根据动能定理求出小球经过最低点时的速度.经过最低点时,由重力和细线的拉力的合力提供小球的向心力,由牛顿第二定律求出细线对小球的拉力.
本题难度:一般