1、计算题  如图所示，为某种材料制成的三棱镜截面ABC，底边BC水平且镀银，其中，∠A=90°，∠B=60°。一束竖直向下的光束，从AB边上的M点入射，经过BC面反射后，从AC边上的N点平行于BC边射出，且MN连线与BC平行。求：
（1）正确作出的光路图；
（2）光线在M点的折射角；
（3）三棱镜的折射率。（可用根式表示）

参考答案：（1）“略”
（2）15°
（3）2/-

本题解析：

本题难度：一般

2、填空题  在做测定玻璃折射率的实验时：

（1）甲同学在纸上正确画出玻璃砖的两个界面ab和cd时，不慎碰了玻璃砖，使它向ab方向平移了一些，如图甲所示，其后的操作都正确，但画光路图时，将折射点确定在ab和cd上，则测出的n值将______．
（2）乙同学为了避免笔尖接触玻璃面，画出的a"b"和c"d"都比实际侧面向外侧平移了一些，如图乙所示，以后的操作均正确，画光路图时将入射点和折射点都确定在a"b"和c"d"上，则测出的n值将______．
（3）丙同学在操作和作图时均无失误，但所用玻璃砖的两面明显不平行，这时测出的n值将______．
（4）图丙是测定某透明媒质折射率的实际记录图，则据此记录，媒质的折射率为______．（可用带刻度的三角板作辅助图，量出数据，算出折射率数值）．

参考答案：（1）用插针法“测定玻璃砖折射率”的实验原理是折射定律n=sinisinr，如图1所示，实线表示玻璃砖向上平移后实际的光路图，虚线表示作图光路图，由图看出，画图时的入射角、折射角与实际的入射角、折射角相等，由折射定律可知，测出的折射率没有变化．即测出的n值将不变．
（2）乙同学画出的ab和cd都比实际侧面向外侧平移了一些，但在画光路图时，将入射点、出射点分别确定在ab、cd上，如图2，实线表示实际的光路图，虚线表示乙同学画图时光路图，入射角测量没有误差，而折射角偏大，则根据折射定律得知，测出的折射率n将偏小．

（3）丙同学所用玻璃砖的两个界面明显不平行，在操作时和作图时均无失误，入射角与折射角没有误差，故测出的n值将不变．
（4）用带刻度的三角板作辅助图，量出数据，结合几何知识知入射角为45°，折射角为30°，故n=sinisinr=

本题解析：

本题难度：简单

3、计算题  如图所示，一根长直棒AB竖直地插入水平池底，水深a=0.8m，棒露出水面部分的长度b=0.6m，太阳光斜射到水面上，与水面夹角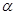=37°，已知水的折射率n=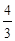，sin37°=0.6，cos37°=0.8．求：

①太阳光射入水中的折射角β；
②棒在池底的影长l．

参考答案：①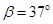②

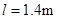
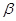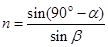本题解析：①设折射角为，则 （2分）
代入数据解得 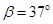    （1分）
②影长  （1分）
代入数据解得 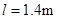   （1分）

考点：光的折射

本题难度：一般

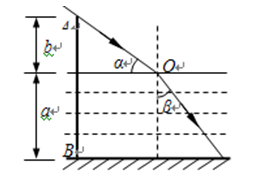
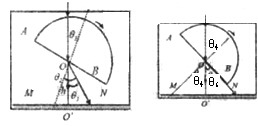
4、计算题  如图所示，折射率n1=1.5的半圆形玻璃砖置于光屏MN的止方。整个装置置于盛满折射率为n2=1.5的液体的容器中，其平面AB到MN的距离为h=20cm。一束单色光沿图示方向射向圆心O，经玻璃砖后射到光屏上的O点。现使玻璃砖绕圆心O点顺时针转动。

①当玻璃砖转过30°时，求射到光屏上的光点到的距离x；
②求射到光屏上的光点离的最远距离；

参考答案：①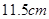②

本题解析：①当玻璃砖转过30°时，如图
又有相对折射率公式得：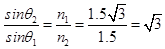

又由几何关系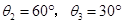得：，解得：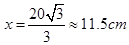
②当最远时是光发生全反射时此时临界角为θ4，由全反射定律得：，故有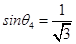
由几何关系得最远距离

本题难度：一般

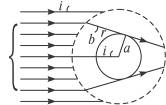
5、简答题  用折射率为n的透明物质做成内、外半径分别为a、b的空心球，如图所示，球的内表面涂有能完全吸收光的物质.则当一平行光射向此球时，球吸收的光束的横截面积多大（指光束进入空心球前的横截面积）？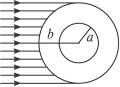

参考答案：πn2a2

本题解析：如图，所括范围内的光线将被球的内表面完全吸收，横截面是一个圆，半径是b·sini；在外表面处发生折射n=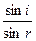，其中sinr=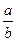，所以球吸收的光束的横截面积是π(b·n·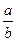)2=πn2a2.

本题难度：简单