1、简答题  如图是磁流体发电机的原理示意图，通道的上、下两个面是两块平行金属板，水平放置，通道的横截面积是边长为d的正方形．匀强磁场的方向垂直前、后两个侧面（即垂直图中纸面向里），磁感应强度为B．一等离子体（即高温下电离的气体，含有大量带正电与负电的微粒，而从整体来说呈电中性）以速度v流过通道，这时两金属板上就聚集电荷，产生电压．已知发电机的等效内阻为r，负载电阻为R．试求：
（1）发电机的电动势；
（2）发电机的总功率和输出功率．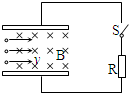

参考答案：（1）设电动势为E，依题意：Bqv=qUd，则路端电压为：U=Bvd
则电动势E=UR（R+r）=Bdv(R+r)R
（2）设总功率为P
P=IE
I=ER+r
总功率：P=EI=E2R+r=B2d2v2(R+r)R2
输出功率为：P1=UI=Bdv?BdvR=B2d2v2R
答：（1）发电机的电动势为Bdv(R+r)R；
（2）发电机的总功率和输出功率为B2d2v2R．

本题解析：

本题难度：一般

2、计算题  如图所示，x轴的上方存在方向与x轴成45°角的匀强电场，电场强度为E，x轴的下方存在垂直纸面向里的匀强磁场，磁感应强度B=0.5 T。有一个质量m=10-11 kg，电荷量q=10-7 C的带正电粒子，该粒子的初速度v0=2×103 m/s，从坐标原点O沿与x轴成45°角的方向进入匀强磁场，经过磁场和电场的作用，粒子从O点出发后第四次经过x轴时刚好又回到O点处，设电场和磁场的区域足够宽，不计粒子重力，求：
(1)带电粒子第一次经过x轴时的横坐标是多少？
(2)电场强度E的大小及带电粒子从O点出发到再次回到O点所用的时间。

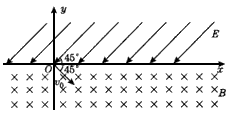
参考答案：解：(1)粒子在磁场中受磁场力的作用沿圆弧运动，洛伦兹力提供向心力qvB=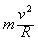
半径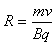=0.4m
根据圆的对称性可得粒子在磁场中第一次偏转所对的圆心角90°，则第一次经过x轴时的横坐标
?
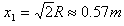(2)粒子第一次进入电场，运动方向与电场方向相反，做匀减速直线运动，速度减为零后又反向加速返回磁场，在磁场中沿圆周运动，再次进入电场时速度方向刚好垂直电场方向，在电场力的作用下偏转，打在坐标原点O处，其运动轨迹如图所示

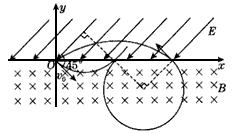
由几何关系可得
第二次进入电场中的位移为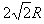
在垂直电场方向的位移s1=vt1
运动时间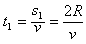=4×10-4 s
在沿电场方向上的位移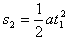
又因s2=2R
得=1×107 m/s2
根据牛顿第二定律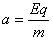
所以电场强度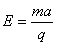=1×103 V/m
粒子从第一次进入电场到再返回磁场的时间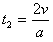=4×10-4 s
粒子在磁场中两段运动的时间之和刚好做一个完整圆周运动的周期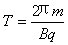=4π×10-4 s
所以粒子从出发到再回到原点所用的时间为t=t1+t2+T≈2.1×10-3 s

本题解析：

本题难度：困难

3、选择题  空间存在如右图所示的匀强电场E和匀强磁场B.下面关于带电粒子在其中运动情况的判断，正确的有(　　)

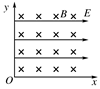
A．若不计重力，粒子做匀速运动的方向可沿y轴正方向，也可沿y轴负方向
B．若不计重力，粒子可沿x轴正方向做匀加速直线运动
C．若重力不能忽略，粒子不可能做匀速直线运动
D．若重力不能忽略，粒子仍可能做匀速直线运动

参考答案：D

本题解析：若不计重力，当粒子沿y轴正方向运动，所受电场力和洛伦兹力方向水平相反，可能做匀速直线运动，其它方向不可能。若重力不能忽略，若带正电粒子向右上方运动或带负电粒子向左上方运动，三个力合力可能为零，可能做匀速直线运动。答案选D。

本题难度：简单

4、选择题  在如图所示的空间中,存在场强为E的匀强电场,同时存在沿x轴负方向?磁感应强度为B的匀强磁场,一质子(电荷量为e)在该空间恰沿y轴正方向以速度v匀速运动.据此可以判断出(? )

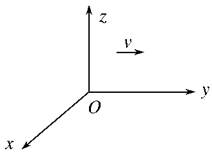
A．质子所受电场力大小等于eE,运动中电势能减小;沿z轴正方向电势升高
B．质子所受电场力大小等于eE,运动中电势能增大;沿z轴正方向电势降低
C．质子所受电场力大小等于evB,运动中电势能不变;沿z轴正方向电势升高
D．质子所受电场力大小等于evB,运动中电势能不变;沿z轴正方向电势降低

参考答案：C

本题解析：根据粒子匀速运动特点可知,电场力等于洛伦兹力.粒子沿着等势线运动,故电势能不变,电场方向沿z轴向下,故ABD错,C正确.

本题难度：一般

5、计算题  在xoy 平面第Ⅰ、Ⅱ象限中，存在沿y轴负方向的匀强电场，场强为E=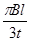，在第Ⅲ、Ⅳ象限中,存在垂直于xoy平面方向如图所示的匀强磁场，磁感应强度B2 =" 2" B1 =" 2" B ，带电粒子a、b先后从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M(0,-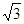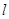)处发生正碰（即碰前两粒子速度方向相反），碰撞前带电粒子b的速度方向与y 轴正方向成60°角，不计粒子重力和两粒子间相互作用。求：

（1）两带电粒子的比荷及在磁场中运动的轨道半径；
（2）带电粒子释放的位置P、Q两点坐标及释放的时间差。

参考答案：（1）?、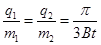
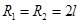
（2）P、Q两点的坐标分别为（l、2l）（-3l、8l）?时间差为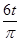

本题解析：（1）由题知a、b两带电粒子在M处发生正碰，其运动轨迹如图，由图可得：

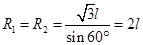
带电粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，进入磁场时的速度为则
，可得

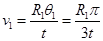
解得：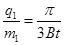
同理可得：
（2）由题可得：对P点释放的粒子有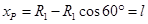
粒子由静止释放做匀加速直线运动，进入磁场时的速度为
加速度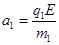
由匀变速直线运动规律得
解得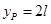，则P点坐标为（l、2l）
同理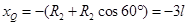



解得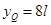，则Q点坐标为（-3l、8l）
带电粒子释放的时间差为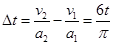

点评：本题关键是由带电粒子在M处发生正碰，画出粒子匀速圆周运动的轨迹，利用几何知识找出圆心及相应的半径。从而找到圆弧所对应的圆心角．由圆心和轨迹用几何知识确定半径是研究带电粒子在匀强磁场中做匀速圆周运动的重要方法．

本题难度：一般