1、简答题  质量为M=It的重锤由静止自由下落1.8 cm后打到要加工的工件上，重锤打到工件上经0.1 s静止不动，试求重锤打到工件上时对工件的平均作用力.（取g="10" m/s2）

参考答案：作用力是70 000 N，方向向下.

本题解析：重锤打击工件的整个过程可分为两个阶段.第一阶段是重锤自由落体运动，下落的时间和与工件接触瞬间的速度可求.第二阶段是重锤打击工件，时间已知，这是研究力、力作用时间和物体运动状态变化的问题，应使用动量定理分析，在哪一段时间范围内使用动量定理呢？一种方法是对重锤打击工件的0.1 s时间内使用动量定理；另一种方法是从重锤开始自由下落到重锤打击工件结束，这一整个过程使用动量定理.哪种方法比较好，通过下面分析就可以看出来.
方法一：重锤下落1.8 m时的速度v=m/s="6" m/s重锤打击工件时，重锤受到向下的重力mg和工件对它向上的力N的作用，对重锤打击工件这段时间使用动量定理，取向上为正方向，重锤受到的总冲量为Nt-mgt，动量的增量为0-mv，根据动量定理有：Nt-mgt=0-mv，工件对重锤的作用力：N=mg-=［1 000×10-］N="70" 000 N.根据牛顿第三定律，重锤对工件的作用力为70 000 N，方向向下.
方法二：重锤下落时间为t0=s="0.6" s，重锤在自由下落过程中只受重力mg，重锤打击工件阶段受到向下的重力mg和工件对它向上的作用力N.对从重锤开始下落到打击工件结束的整个过程使用动量定理，以向下为正方向，重锤受到的冲量总和为mg(t0+t)-Nt，重锤初、末状态的动量均为零.根据动量定理，有：
mg(t0+t)-Nt=0，N=="1" 000×10×(0.6+0.1)/0.1 N="70" 000 N，根据牛顿第三定律，重锤打击工件的作用力是70 000 N，方向向下.上述两种方法中，动量定理使用的范围不同，但最终结果相同.两种方法比较第二种解法比较简单.

本题难度：简单

2、简答题  

（1）在被第二颗子弹击中前,木块沿斜面向上运动离A点的最大距离?
（2）木块在斜面上最多能被多少颗子弹击中?
（3）在木块从C点开始运动到最终离开斜面的过程中,子弹、木块和斜面一系统所产生的内能是多少?

参考答案：(1) 12.5m (2) 3颗(3)10434J

本题解析：（1）木块下滑的加速度为：

第一颗子弹射入前木块的速度：
木块向下运动的距离：
第一颗子弹射入时动量守恒，射入后木块的速度v2，?
解得：
木块向上运动的加速度大小：
木块向上运动的最大距离：
只需1秒，木块的速度就为零，第二颗子弹还未射出，所以离A点最大距离：

（2）由于每颗子弹击中产生的效果相同，上升4米，下降0.5米，一个周期上升3.5米，故只能被3颗子弹击中
（3）物块在斜面上运动的v-t的图像如右图
物块从C到离开的路程：
摩擦力做功产生的热量：

子弹打入时产生的热量：

产生的总热量：

本题难度：一般

3、简答题  如图6-18所示，甲、乙两人做抛球游戏，甲站在一辆平板车上，车与水平地面间的摩擦不计．甲与车整体的质量为M＝100kg．另有一质量为m＝2kg的球．乙站在车对面的地上，身边有若干个质量不等的球，开始时车静止，甲将球以速度v（相对地面）水平抛给乙，乙接到抛来的球后，马上将另一质量为的球以相同的速度v（相对地面）水平抛回给甲，甲接住后再以相同速率v将此球水平抛给乙，这样往复进行，乙每次抛回给甲的质量都在它接到的球的质量上加一个m，球在空中认为始终做直线运动，求：

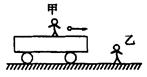
图6-18
　　（1）甲第二次抛出球后车的速度大小?
　　（2）从第二次算起，甲抛出多少个球后不能接到乙抛回来的球?

参考答案：（1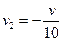）（2）第7次抛出球后不能接到乙抛回来的球

本题解析：（1）以球、甲和车作为系统　第一次抛球：（抛后甲与车速度）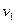
　　第二次抛球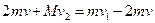：　第三次抛球：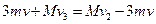
　　第n次抛球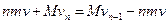：　相加后得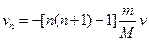
　　当n＝2时，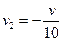
　　（2）欲使车上的人再不能接到乙抛回来的球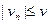，有，即有，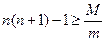
　　解得n≥6.7　故甲第7次抛出球后不能接到乙抛回来的球．

本题难度：一般

4、计算题  如图，半径R=0.8m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点D与长为L的水平面相切于D点，质量M=1.0kg的小滑块A从圆弧顶点C由静止释放，到达最低点D点后，与D点m=0.5kg的静止小物块B相碰，碰后A的速度变为vA="2.0" m/s，仍向右运动．已知两物块与水平面间的动摩擦因数均为µ=0.1，A、B均可视为质点，B与E处的竖直挡板相碰时没有机械能损失，取g=10m/s2．求：

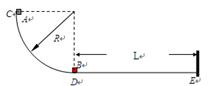
（1）滑块A刚到达圆弧的最低点D时对圆弧的压力；
（2）滑块B被碰后瞬间的速度；
（3）要使两滑块能发生第二次碰撞，DE的长度L应满足的条件．

参考答案：（1）F＝30 N（2）vB＝4 m/s（3）L＜5m

本题解析：（1）设小滑块运动到D点的速度为v，由机械能守恒定律有：MgR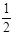＝Mv2 (2分)
在D点，由牛顿第二定律有：F - Mg＝M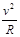  (2分)
联立得： F＝30 N  (1分)
由牛顿第三定律，小滑块在D点时对圆弧的压力为30N  (1分)
(2) 设B滑块被碰后的速度为vB，由动量守恒定律：M v＝MvA+mvB   (3分)
得： vB＝4 m/s  （1分）
(3) 由于B物块的速度较大，如果它们能再次相碰一定发生在B从竖直挡板弹回后，假设两物块能运动到最后停止，达到最大的路程，则
对于A物块，由动能定理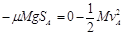：  (2分)
解得：SA="2" m  （1分）
对于B物块，由于B与竖直挡板的碰撞无机械能损失，由动能定理：
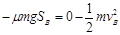     (2分)
解得：SB="8" m（1分）
两滑块刚好第二次发生接触的条件2L=SA+ SB="10" m  （1分）
要使两滑块能发生第二次碰撞L＜5m （1分）
考点：考查了动能定理，动量守恒定律，牛顿运动定律

本题难度：困难

5、计算题  科学家设想在未来的航天事业中用太阳帆来加速星际宇宙飞船，按照近代光的粒子说，光由光子组成，飞船在太空中张开太阳帆，使太阳光垂直射到太阳帆上，太阳帆面积为S，太阳帆对光的反射率为100%，设太阳帆上每单位面积每秒到达n个光子，每个光子的动量为p，如飞船总质量为m，求飞船加速度的表达式．

参考答案：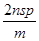

本题解析：根据动量定理，，，加速度为 a=。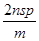
先利用动量定理求出力，再根据牛顿第二定律求解。

本题难度：简单