1、计算题  如图所示，木块质量m＝0.78 kg，在与水平方向成q＝37°角、斜向右上方和恒定拉力F作用下，以a＝2.0 m/s2的加速度从静止开始做匀加速直线运动，在3 s末时撤去拉力F。已知木块与地面间的动摩擦因数m＝0.4，取重力加速度g＝10 m/s2，sin37°＝0.6，cos37°＝0.8。求：（1）拉力F的大小（2）物体在5 s内滑行的总位移。

参考答案：4.5 N ，13.5m

本题解析：（1）以物体为研究对象，进行受力分析可知竖直方向上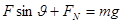，在水平方向上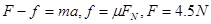（2）在前3s内，物体走过的位移为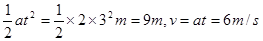，撤去拉力F后，加速度由滑动摩擦力提供，为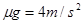，可知物体减速1.5s后静止，因此撤去F后的位移为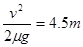，总位移为13.5m
点评：本题难度较小，分析受力情况是关键，加速度为水平方向，撤去拉力F后，物体做的是减速直线运动，要先判读出在5s时物体的速度是否已经减小到零

本题难度：简单

2、简答题  在水平面上有一质量为4kg的物体，在水平拉力F=9N的作用下由静止开始运动，10s后速度达到10m/s，然后撤去拉力，求：
（1）物体与地面间的动摩擦因数μ；
（2）物体在撤去拉力后经过多长时间停下；
（3）物体从开始运动到最后停下，总共的位移是多大？

参考答案：（1）物体在F作用下由静止开始做匀加速直线运动过程，由v=a1t1，得 a1=vt1=1010m/s2=1m/s2
由牛顿第二定律得? F-μmg=ma1，得
? μ=F-ma1mg
代入解得，μ=0.125?
（2）撤去F后，物体的加速度大小为? a2=μmgm=1.25m/s2，
滑行时间为 t2=va2=8s
（3）物体从开始运动到最后停下，总共的位移是 x=v2(t1+t2)=102×18m=90m
答：
（1）物体与地面间的动摩擦因数μ是0.125；
（2）物体在撤去拉力后经过8s时间停下；
（3）物体从开始运动到最后停下，总共的位移是90m．

本题解析：

本题难度：一般

3、选择题  如图所示是做直线运动的甲、乙物体的位移-时间图象，由图象可判断下列说法中不正确的是（　　）
A．当t=t2时两物体相距最远
B．当t=t2时两物体相遇
C．甲起动的时间比乙早t1秒
D．当t=t3时两物体相距S0米