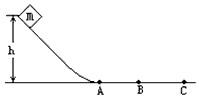
1、填空题  如图所示，质量为m的物块从高h的斜面顶端由静止开始滑下，最后停止在水平面上B点。若物块从斜面顶端以初速度v0沿斜面滑下，则停止在水平面的上C点，已知AB=BC，则物块在斜面上克服阻力做的功为__________。（设物块经过斜面与水平面交接点处无能量损失）。

参考答案：mgh－1/2mv22

本题解析：

本题难度：一般

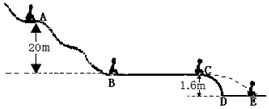
2、计算题  如图所示为某娱乐场的滑道示意图，其中AB为曲面滑道，BC为水平滑道，水平滑道BC与半径为1.6m的1/4圆弧滑道CD相切，DE为放在水平地面上的海绵垫。某人从坡顶滑下，经过高度差为20m的A点和B点时的速度分别为2m/s和12m/s，在C点做平抛运动，最后落在海绵垫上E点。人的质量为70kg，在BC段的动摩擦因数为0.2。问：
（1）从A到B的过程中，人克服阻力做的功是多少？
（2）为保证在C点做平抛运动，BC的最大值是多少？
（3）若BC取最大值，则DE的长是多少？

参考答案：解：（1）由动能定理：
得：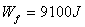
（2）BC段加速度为：
设在C点的最小速度为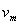，由，
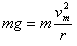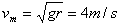
BC的最大值为：，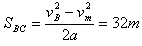
BC的长度范围是0--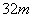
（3）平抛运动的时间：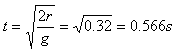
BC取最大长度，对应平抛运动的初速度为
平抛运动的水平位移：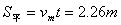
DE的长：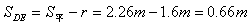

本题解析：

本题难度：困难

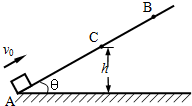
3、简答题  如图，让一小物体（可看作质点）从图示斜面上的A点以v0=4m/s的初速度滑上斜面，物体滑到斜面上的B点后沿原路返回．若A到B的距离为1m，斜面倾角为θ=37°．（sin37°=0.6，cos37°=0.8，g=10m/s2）
（1）求物体与斜面间的动摩擦因数；
（2）若设水平地面为零重力势能面，且物体返回经过C点时，其动能恰与重力势能相等，求C点相对水平地面的高度h．

参考答案：（1）设物体与斜面间的滑动摩擦因数为μ，则物体上滑由A到B做速度由v0变为0的匀减速运动，由动能定理有
-mgssinθ-μmgscosθ=0-12mv2，代入数据解得μ=0.25
（本题也可用牛顿运动定律求由牛顿第二定律有mgsinθ+μmgcosθ=ma…①，
又由运动学公式，可得0-v02=-2a?AB…②，
由①②联立，代入数据可得μ=0.25）
即物体与斜面间的动摩擦因数为0.25．
（2）设物体返回经过C点时速度大小为v1，则对于物体由B到C，
由动能定理有mg（ABsinθ-h）-μmgcosθ.AB．sinθ-hsinθ=12mv2
又12mv2=mgh，
联立以上两式解得h=sinθ-μcosθ2-μcosθAB
代入数据可得：h=0.24m
即动能与势能相等时C点相对地面的高度为0.24m．

本题解析：

本题难度：一般

4、计算题  （9分）如图所示，光滑水平路面上，有一质量为m1=5kg的无动力小车以匀速率v0=2m/s向前行驶，小车由轻绳与另一质量为m2=25kg的车厢连结，车厢右端有一质量为m3=20kg的物体（可视为质点），物体与车厢的动摩擦因数为μ=0.2，开始物体静止在车厢上，绳子是松驰的．求：

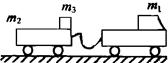
①当小车、车厢、物体以共同速度运动时，物体相对车厢的位移（设物体不会从车厢上滑下）；
②从绳拉紧到小车、车厢、物体具有共同速度所需时间．（取g=10m/s2）

参考答案：①0.017 m　　　②0.1s

本题解析：①轻绳从伸直到拉紧的时间极短，在此过程中，物体可认为仍处于静止状态，小车与车厢在水平方向上动量守恒，设小车与车厢的共同速度为，以m1和m2为研究对象，由动量守恒定律有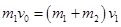
解得．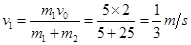
绳拉紧后，物体在车厢上发生相对滑动，最终小车、车厢和物体三者相对静止，具有共同速度．再将小车、车厢和物体三者看成一系统，在水平方向上动量守恒，以m1、m2、m3为对象，设它们最后的共同速度为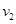，则由动量守恒定律有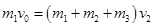
解得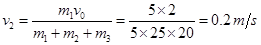　
绳刚拉紧时m1和m2的速度为v1，最后m1、m2、m3的共同速度为v2，设m3相对m2的位移为Δx，则在此过程中由能量守恒定律有

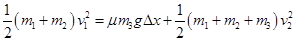
解得：．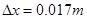
②对物体，由动量定理，有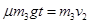　　
解得：
所以，从绳拉紧到m1、m2、m3有共同速度所需时间为t = 0.1s．

本题难度：一般

5、实验题  如图16所示，当磕头虫背朝下射在地面时，它会弓起它的背向上突然弹起，而将体内储存的能量转变成机械能。这样的弹射动作会发出嗒嗒响声，因而使此虫得名。磕头虫弹射的录像显示，一个质量为m=4.0×10-6kg的磕头虫的质心在弓背过程中直接上升了0.77mm，弹射达到的最大高度有h=0.30m。在它的弹射过程中，地面对磕头虫所施的外力的平均值是多少？

参考答案：1.5×10-2N

本题解析：在弹射过程中磕头虫的内能转变为其相对地面的机械能，在磕头虫在弹离地面瞬间和在空中上升过程中机械能守恒，设其上升的初速度为v1?图16
上升的最大高度为h，则有：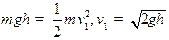
设磕头虫在开始弹射到离开地面这段时间内地球给它的平均作用力是F，则由动能定理得;

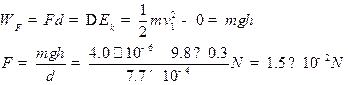
本题难度：一般